Preliminaries of IMU Preintegration (2) Uncertainty Description in SO(3)

원 논문의 이름이 “On-Manifold Preintegration for Real-Time Visual-Inertial Odometry”인만큼 preintegration을 이해하기 위해서는 manifold에 대한 이해를 필요로 한다. 하지만 수학 위주의 엄밀한 증명보다는 본 글에서는 왜 SO(3)를 쓰는 게 용이한지에 좀 더 초점을 맞추어 간단히 설명을 한다.

Rotation from 2D to 3D

3D 공간 상에서 Rotation을 표현하는 방법이라고 하면 크게

a) Euler angle representation,
b) Quaternion,
c) Lie Group, i.e. SO(3)

를 떠올릴 것이다. 이 세 가지에 대해 친숙하지 않더라도 괜찮다. 사실 우리는 교육과정에서 2D 공간 상의 회전에 대한 여러 표현 방식에 대해 알게 모르게 배웠는데, 개인적인 생각으로는 2D 상의 회전을 표현하는 방식과 3차원 공간 상에서 회전을 표현하는 방식은 아래와 같은 대응관계를 지닌다고 생각하고, 각각의 특징 또한 간략히 적어두었다.

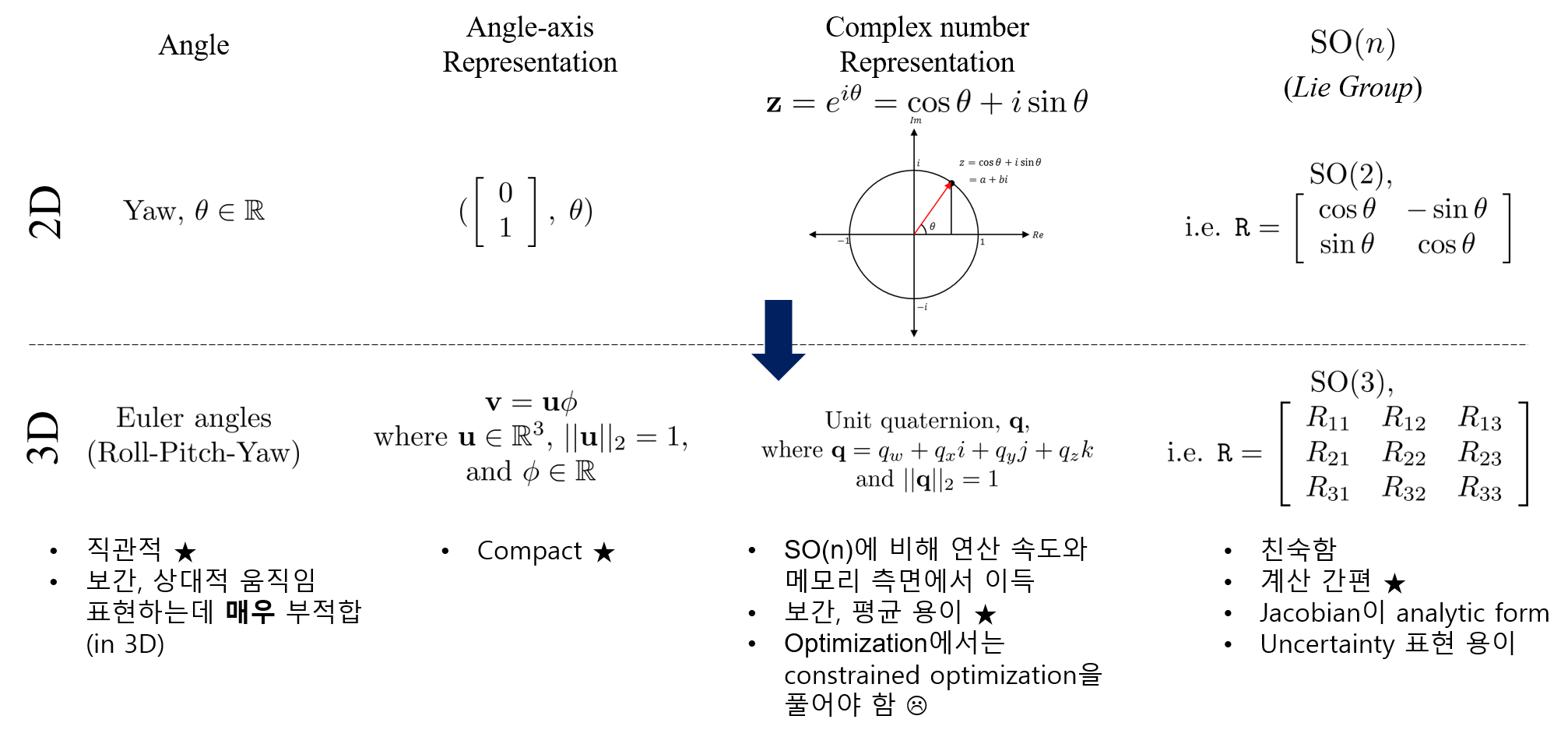
Rotation에 대해 자세히 설명하면 글이 너무 길어지기 때문에 자세한 설명글은 여기(TBU) 에서 다룬다.

무튼, 기억해야할 것은 rotation term에 대한 optimization을 할 때는 SO(3)를 angle-axis representation으로 parametrization하여 푸는데, 이러한 행위를 하는 데에는 세 가지 장점이 있다.

3x3 rotation matrix를 표현하려면 6개의 parameter가 필요한 반면, axis-angle representation으로 rotation을 표현하면 3개의 parameter만으로 3D rotation을 표현할 수 있다. 그렇다면 ‘왜 quaternion’으로는 표현을 안 하냐’는 궁금증이 있을 수 있는데, quaternion으로 parametrization을 하면 optimization을 할 때 상당히 까다롭기 때문이다. quaternion은 크기가 1이어야 한다는 constraint가 있는데, 이 constraint를 유지하면서 optimization의 결과를 quaternion으로 update하려면 constrained optimization을 풀어야 한다. 이는 angle-axis representation으로 rotation을 표현한 후 optimization을 하는 것에 비해 상당히 까다롭다.
주로 optimization을 할 때는 iterative하게 푸는데, 만약 rotation의 변화량의 크기가 작다면, i.e. 위의 표 상에서 \(\mathbf{v}\)의 크기가 작다면, \(\text{Exp}(\mathbf{v}) \backsimeq \mathbf{I}_3 + [\mathbf{v}]_{\times}\)로 approximation이 쉽게 가능하다.
Rotation의 불확실성 (uncertainty)를 표현하는 것이 용이해진다. 이러한 표현은 기존의 Euclidean geometry 상에서 사용하던 linear equation이나 non-linear equation에 uncertainty를 표현할 때 gaussian noise를 더해주는 행위와 같은 의미로서 사용이 가능하다. 자세한 내용은 이어서 마저 설명한다.

Uncertainty Description in SO(3)

On-Manifold Preintegration를 이해하는 데 가장 핵심적이고 중요한 개념이 논문 내의 Section Ⅲ. B에서 소개되는, SO(3)의 uncertainty에 관련된 내용이다. 겉보기에는 논문에서도 preliminaries에 있어서 별로 안 중요하겠거니 했는데 이 부분의 의미를 깨닫는 것이 제일 중요하다. SO(3)의 uncertainty를 표현하는 것에 대해 받아들이지 못 하면 뒤의 Section에서 전개를 통해 preintegrated measurements를 구하는 과정을 왜 하고 있는지 이해할 수 없기 때문이다.

3차원 상에서의 회전에 대한 uncertainty는 기존 noise-free인 rotation matrix와 uncertainty vector \(\epsilon \in \mathbb{R}^3\)를 exponential map을 통해 투영한 rotation matrix의 곱으로 아래와 같이 표현이 가능하다 (SO(3) \(\times\) SO(3) → SO(3)):

\[\tilde{\mathtt{R}}=\mathtt{R} \operatorname{Exp}(\epsilon), \quad \epsilon \sim \mathcal{N}(0, \Sigma) \; \; \; \; \text{[1]}\]

즉, 위의 식은 3차원 공간 상의 회전을 표현하는 manifold에 대한 uncertainty를 3x1 크기를 지니고 zero-mean인 gaussian distribution으로 표현할 수 있음을 뜻한다.

이는 graph SLAM을 할 때 상당히 중요하다. 일반적으로 \(i\) 번째 keyframe과 \(j\) 번째 keyframe 사이의 어떤 error term을 \(\mathbf{e}_{i j}\)라 하고, 그에 해당하는 uncertainty를 \(\Omega_{i j}\)라 했을 때 Factor graph SLAM의 최종 목표는 아래의 optimization 수식을 푸는 것과 같다:

\[\mathbf{x}^{*}=\operatorname{argmin} \sum_{\mathbf{x}} \mathbf{e}_{i j}^{T} {\Omega}_{i j} \mathbf{e}_{i j} \; \; \; \; \; \; \text{[2]}\]

즉, graph SLAM을 하기 위해서는 residual \(\mathbf{e}_{i j}\)와 그 residual의 uncertainty \(\Omega_{i j}\)를 수학적으로 표현해야 하는데, 수식 [1]을 통해 [2]의 \(\Omega_{ij}\)에 대응되는 부분 (어려운 말로는 information matrix라 부름)의 표현이 가능해진다 (i.e. \(\epsilon\)이 크다 → rotation에 대한 measurements가 불확실하다는 의미 → 해당 measurements에 해당하는 error 크기의 중경도를 따질 때 덜 중요하다고 여김, i.e. 지닌 information의 중요한 정도가 낮다고 판단).

이 개념을 잘 받아들이는 게 중요한데, 왜냐하면 이 논문의 Section Ⅵ에서 설명하는 preintegration on manifold에서 최종적으로 증명하고자 하는 것이 keyframe \(i\)와 \(j\)의 사이의 수십~수백 여개의 IMU measurements를 \(i\)와 \(j\) 간의 하나의 \(\epsilon\) term로 간략화하는 것이기 때문이다. 더 자세한 것은 Derivation of Preintegrated IMU Measurements 파트에서 다루니, “3D 공간 상의 rotation의 uncertainty를 exponential map을 활용하여 표현함으로써 기존의 factor graph SLAM framework를 그대로 사용해서 optimization하는 것이 가능하다“는 정도만 기억해주면 좋을 것 같다.

IMU Preintegration Derivation 설명 시리즈입니다.