Derivation of IMU Model and Motion Integration
Integration 한줄 요약
The goal now is to infer the motion of the system from IMU measurements. For this purpose we introduce the following kinematic model
(의역) 먼저 preintegration에 대해 살피기 전에 아래와 각 IMU 사이의 motion을 어떻게 intergration을하는 지 해당 section에서 살펴 본다.
(본 내용은 Section Ⅴ 내용의 자세한 설명을 하고 있습니다)
IMU Model and Motion Integration
위에서 말했듯이, preintegration에 대해 증명하기 앞서, 먼저 discrete-time system 상에서 Hz가 높은 IMU sensor를 통해 motion을 어떻게 표현할 수 있는지에 대해서 알아본다. 따라서 integration의 최종 목표는 아래의 자주색 화살표에 대응되는 relative rotation, position, velocity를 어떻게 구하는지 살펴본다.
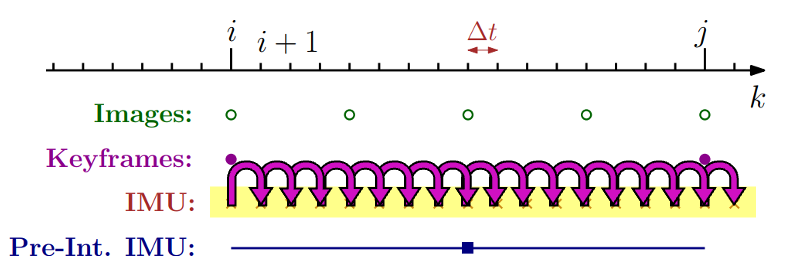
IMU sensor의 특성
Integration을 하기 앞서 먼저 IMU가 제공하는 데이터 타입에 대해 먼저 살펴보자. IMU는 주로 3-axis accelerometer와 3-axis gyroscope로 구성되어 있어 회전하는 속도 (rotation rate or angular velocity)와 병진 운동에 대한 가속도를 측정할 수 있습니다 (물론 3-axis magnetometer까지 추가한 9축 IMU도 있다).
고등학교 물리시간에 배웠듯이 가속도를 적분하면 속도가 되고, 다시 속도를 적분하면 결국 위치를 추정할 수 있다. 하지만 현실 세계의 IMU sensor가 제공하는 가속도는 생각보다 호락호락(?)하지 않다. 그 이유는 아래와 같이 세 개로 꼽을 수 있다.
- a) IMU data는 대체로 아주 많이 noisy하고 bias가 존재한다. 물론, 이러한 현상은 가속도를 취득하는 센서의 원리에 따라서 달라지긴 한다. 예로 들어서 비행기에서 사용하는 수천만원짜리 IMU sensor는 가속도를 mechanical하게 측정하기 때문에 noise의 크기가 상당히 적고 bias도 거의 없다. 하지만 우리의 타겟인 모바일 로봇에는 이러한 IMU sensor를 쓰기에는 무리가 있기 때문에 (가격적으로나 무게적으로나) 주로 MEMS 기반 저가형 IMU를 사용한다. 이러한 MEMS 기반 IMU는 IMU에 작용하는 관성의 정도를 전류의 크기로 변환하는데, 그 과정이 아주 미세하다보니 미세한 떨림에도 전류의 크기가 불규칙적으로 바뀌게 되어 white noise가 존재하게 된다 (이 Youtube의 0:30에 측정 원리가 잘 visualization되어 있음). 그리고 소자를 만드는 과정에서 불순물이나 약간의 치수공차등으로 인해 가속도 → 전류로 변환하는 과정에서 저항이 달라지게 되어 내부에 bias가 필연적으로 생기게 된다.
- b) 지구에는 중력이 존재한다. 따라서 정확한 가속도를 추정하려면 중력의 영향을 제거해주어야 한다.
- c) IMU는 IMU가 부착되어 있는 위치를 기준으로 가속도를 측정한다 (Inertial frame이라고 부르기도 하며, 주로 로봇의 Body frame B와 동일시 되기도 한다). 따라서, 가속도를 활용해 우리의 목표인 World frame의 (x, y, z)를 추정하려면 측정한 가속도를 world 좌표계로 변화해주는 과정이 필요하다.
위의 (b)와 (c)를 더 이해하기 쉽게 아래에 예시 상황을 그려보았다. 아래의 그림과 같이 pitch방향으로 -45도 기울어져있는 상태 (pitch는 World frame의 Y축 방향으로 시계 방향 회전이 +임을 주의)로 드론이 가속운동을 한다고 가정해보자. 드론이 드론 자기자신을 기준으로(Body frame 기준으로) X 방향으로 \(13.873m/s^2\)으로 가속한다고 하면, IMU에서 측정하는 가속도는 위의 가속 움직임으로 발생한 가속도와 중력방향의 가속도의 합이 된다. 그런데 중력은 자명하게도 World frame 기준으로 -Z 방향으로 향하기 때문에 IMU에서 측정하는 가속도를 Body frame 기준으로 변환해주어야 한다. 따라서 실제로 IMU 상에서 관측되는 가속도 \(_\text{B}^\text{Mes}{\mathbf{a}}(t)\)는 noise가 없다는 가정하에 \(_\text{B}^\text{Mes}{\mathbf{a}}(t) = {_\text{B}\mathbf{a}(t) - {\mathtt{R}_{\text{WB}}^\intercal}{_\text{W}\mathbf{g}}}= {\mathtt{R}_{\text{WB}}^\intercal}({_\text{W}\mathbf{a}(t) - {_\text{W}\mathbf{g}})}\)로 표현할 수 있다. 참고로 중력가속도 \(_\text{W}\mathbf{g}\)는 주로 \([0, \; 0, \; 9.81]^\intercal\)로, 양수로 표현된다.
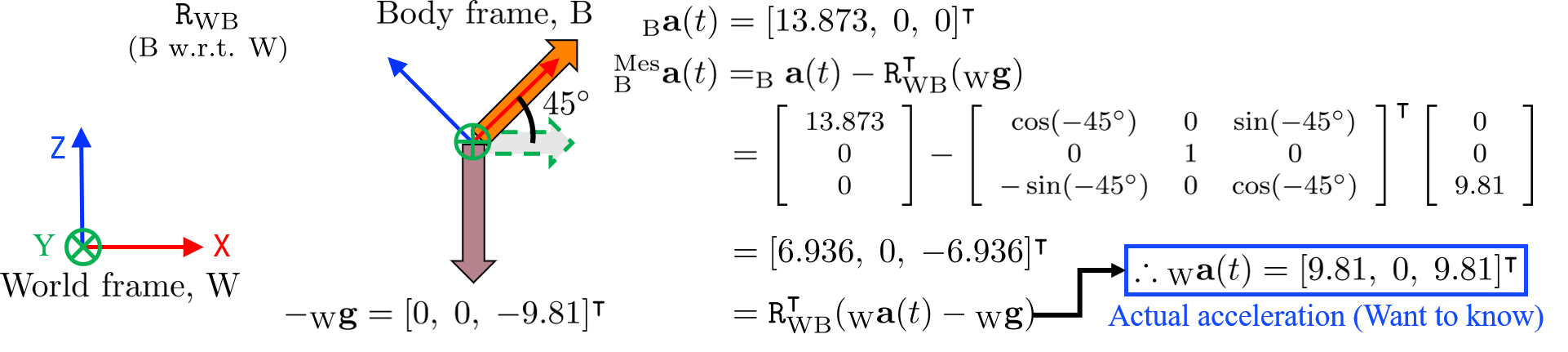
NOTE: 여기서 기억해야할 것은 우리가 최종적으로 구하고 싶은 것은 \(_\text{W}\mathbf{a}(t)\)라는 것이다. 위의 식을 기반으로 bias \(\mathbf{b}\)와 noise \(\boldsymbol{\eta}\)까지 포함시키면 최종적으로 우리가 추정하고자 하는 state들과 IMU에서 noise를 포함하여 측정되는 수식의 관계는 아래와 같이 표현된다.

윗첨자 \(g\)와 \(a\)는 각각 gyroscope와 acceleration을 뜻한다.
Derivation
그 후 아래의 수식전개를 통해 \(t\)일 때와 \(t + \Delta t\)의 상대적 motion을 아래와 같이 전개할 수 있다.

최종적으로 \(i\) 번째 keyframe과 \(j\) 번째 keyframe 간의 모션은 수식 (31)을 활용하여 K개의 IMU measurements를 통해 추정한 미소 움직임을 축적 (intergration)하면 구할 수 있다.
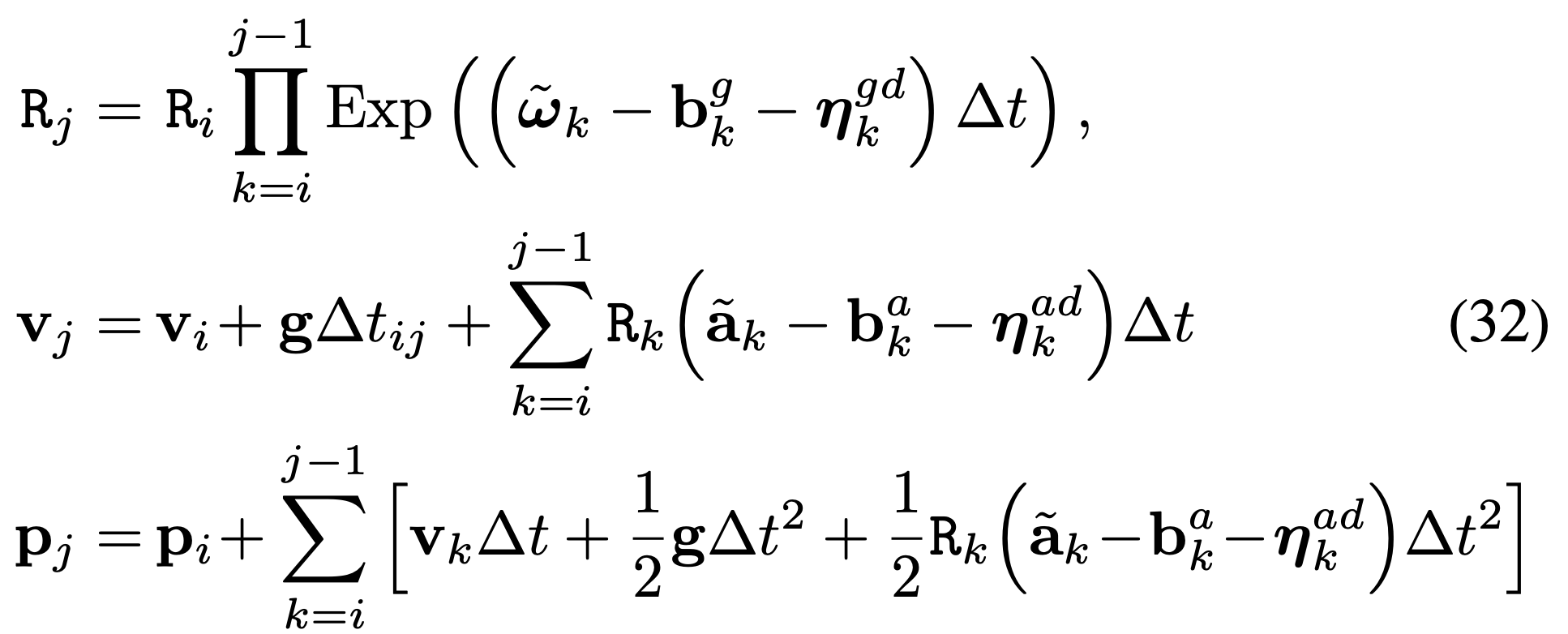
IMU Preintegration Derivation 설명 시리즈입니다.
- IMU Preintegration (Easy) - 1. Introduction
- IMU Preintegration (Easy) - 2. Preliminaries (1) Keyframe
- IMU Preintegration (Easy) - 2. Preliminaries (2) 3D Rotation and Uncertainty
- IMU Preintegration (Easy) - 3. Derivation of IMU Model and Motion Integration
- IMU Preintegration (Easy) - 4. Derivation of Preintegrated IMU Measurements
- IMU Preintegration (Easy) - 5. IMUPreintegration in LIO-SAM