IMU Preintegration (Easy) - 4. Derivation of Preintegrated IMU Measurements

본 글에서는 \(i\)와 \(j\) 번째의 keyframe 사이의 총 K개의 IMU measurement을 어떻게 preintegration하는지에 대해서 설명한다.

Preintegrated IMU Measurements

앞서 유도한 아래의 수식을 다시 살펴보자.

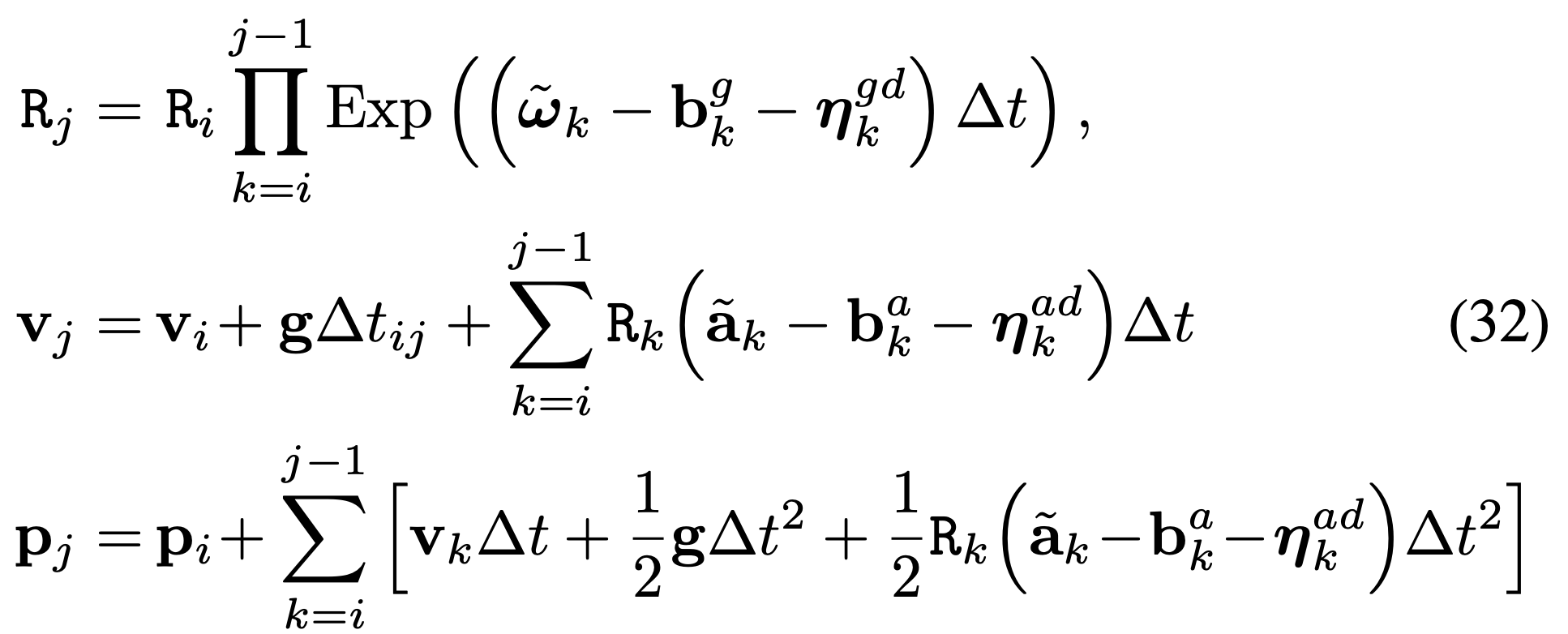
위의 수식에서 \(\mathtt{R}_i\), \(\mathbf{v}_i\), \(\mathbf{p}_i\)를 좌변으로 이항해주면 \(i\) 번째 keyframe과 \(j\) 번째 keyframe 사이의 최종적인 relative motion에 대해 표현할 수 있다. Introduction에서 말했듯이, 위의 수식만을 이용해서 factor graph optimization을 하는 것은 이미 가능하다. 하지만 위의 수식을 이용해서 factor graph optimization을 하면 \(i+1, i+2, \cdots, j-1\)의 pose들 또한 모두 다 parameter로 지니고 있어야 한다. 이는 앞서 말한 것 처럼 연산적인 측면이나 메모리적인 측면이나 모두 다 부담이 된다 (Intro에서 약 25분 동안 데이터를 취득하면 49만 여개의 데이터가 취득된 것을 상기하자).

이러한 문제를 해결하기 위해 논문의 저자는 수백 여개의 measurments를 factor로 직접적으로 넣는 것이 아니라, factor graph에 measurement를 추가하기 이전에 (pre-) 수백여개의 IMU data를 단 하나의 factor로 취합(integration)하는 방법에 대해서 제안한다.

Definition & Assumption

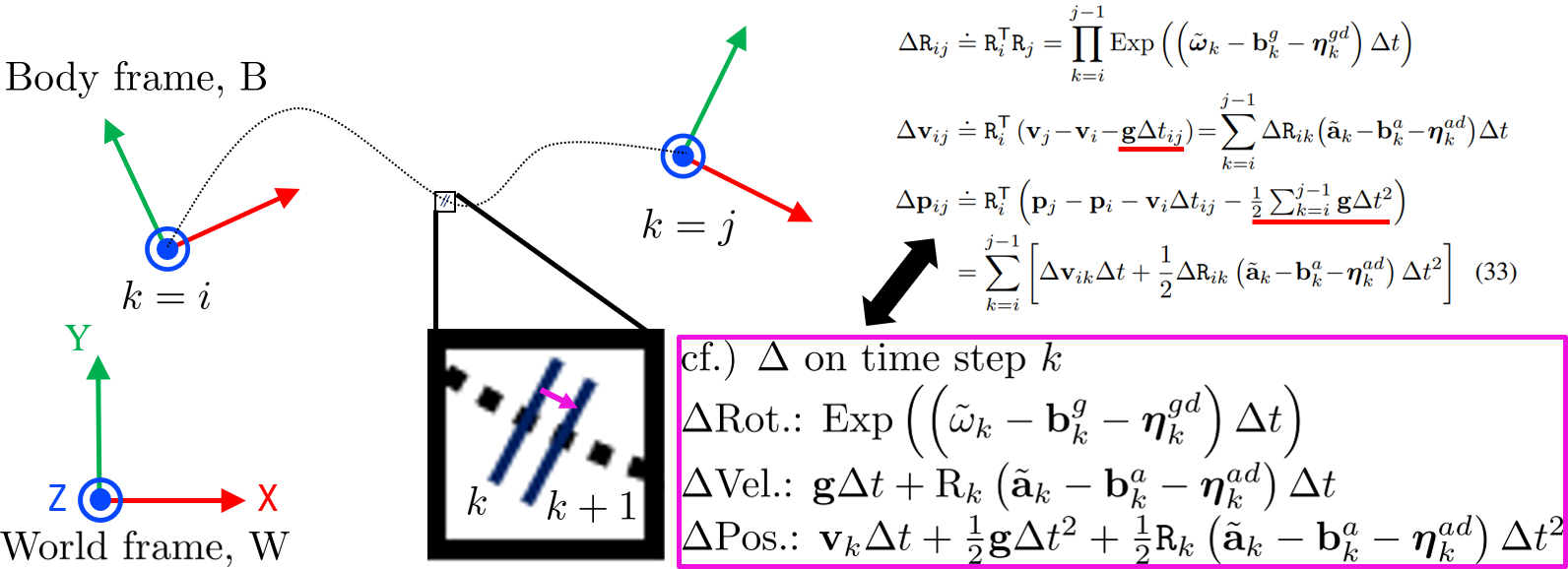
Definition: Preintegration의 과정을 유도하기 앞서 논문에서는 아래와 같이 rotation, velocity, position에 대한 “relative motion increments” \(\Delta \mathtt{R}_{ij}\), \(\Delta \mathbf{v}_{ij}\), \(\Delta \mathbf{p}_{ij}\)를 정의한다:

여기서 \(\Delta t_{ij}\)는 두 keyframe 간의 총 시간 차를 의미한다. 참고로 이 relative motion increments 중 \(\Delta \mathbf{v}_{ij}\)와 \(\Delta \mathbf{p}_{ij}\)는 물리적인 incremental motion을 뜻하지는 않는다. 왜냐하면 전개의 편의성을 위해서 중력에 관련된 term도 좌변으로 이항했기 때문이다. 실제로 \(k\) 번째와 \(k+1\) frame 사이의 물리적인 relative motion (아래의 자주색으로 표시된 부분)은 아래와 같다는 것을 주의하자.

Assumption: 그 후, 수식을 전개하기 전 \(i\) 번째와 \(j\) keyframe 사이에서는 bias가 일정하다고 가정한다.

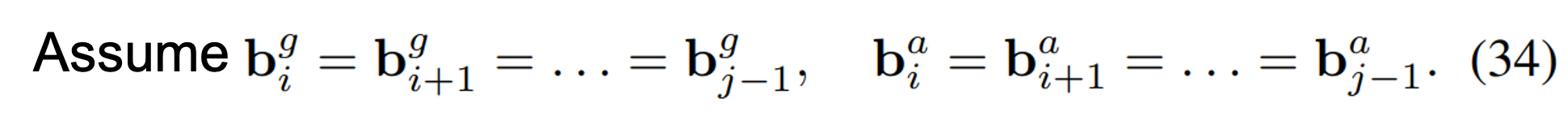
실제로 bias는 주로 MEMS system 상에 전기적 신호의 offset으로 인해 발생하는 것이기 때문에 빠른 시간 내에 급격하게 변화하지 않는다. 따라서 위처럼 가정을 해도 괜찮다.

Derivation of Preintegrated IMU Measurements

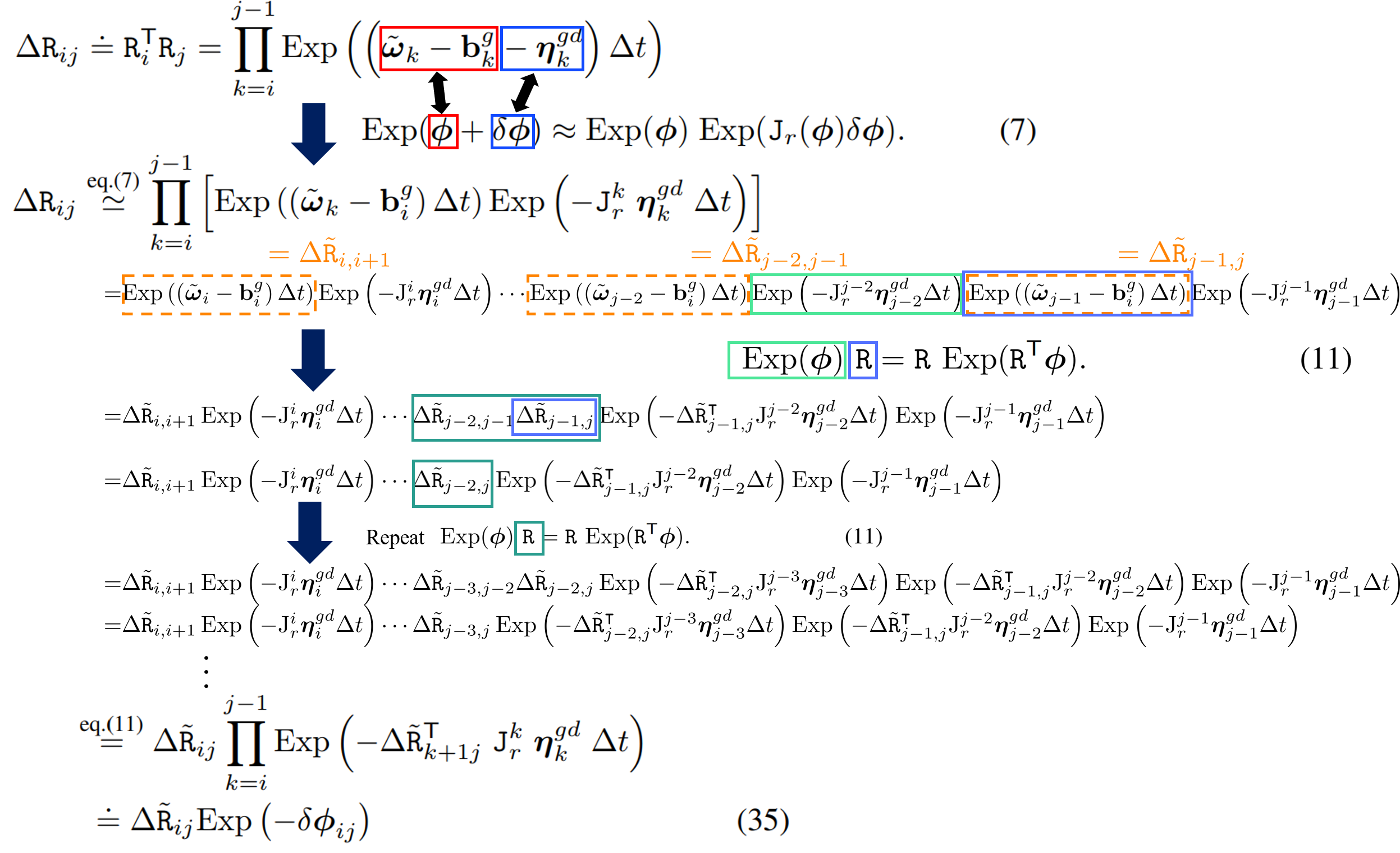
위의 정의와 가정 이후 아래와 같이 실제 relative motion increments와 noise와 bias의 영향을 받은 measured relative motion increments간의 상관관계를 유도한다 (아래 전개가 이해가 안 되시는 분은 Joan Sola의 님의 Quaternion kinematics for the error-state Kalman filter,,,Chapter 4까지,,,꼭 읽어보시길 바랍니다,,,).

Preintegrated Rotation Measurements

Preintegrated Velocity Measurements

Preintegrated Position Measurements

Do the Uncertainties behave like Gaussian distribution?

위의 전개를 하다보면 ‘이걸 왜 하고 있는거지…?’하며 정신이 살짝 아득해지는데, 이제 거의 다 왔다! 위의 전개를 통해 증명하고자 하는 것은 “IMU data로 measured된 relative motion increments는 추정해야하는 (to-be-estimated) relative motion increments과 gaussian distribution을 따르는 random vector의 합의 꼴로 표현이 가능하다”는 것이다.

사실 \(\delta \boldsymbol{\phi}_{ij}\)는 Gaussian의 꼴이 아닌데, \(\boldsymbol{\eta}^{gd}_k\)와 \(\Delta t\)의 값이 아주 작아서 jacobian이 identity matrix \(\mathbf{I}\)로 근사가 가능하다는 것을 활용하면 아래와 같이 approximation을 할 수 있다:

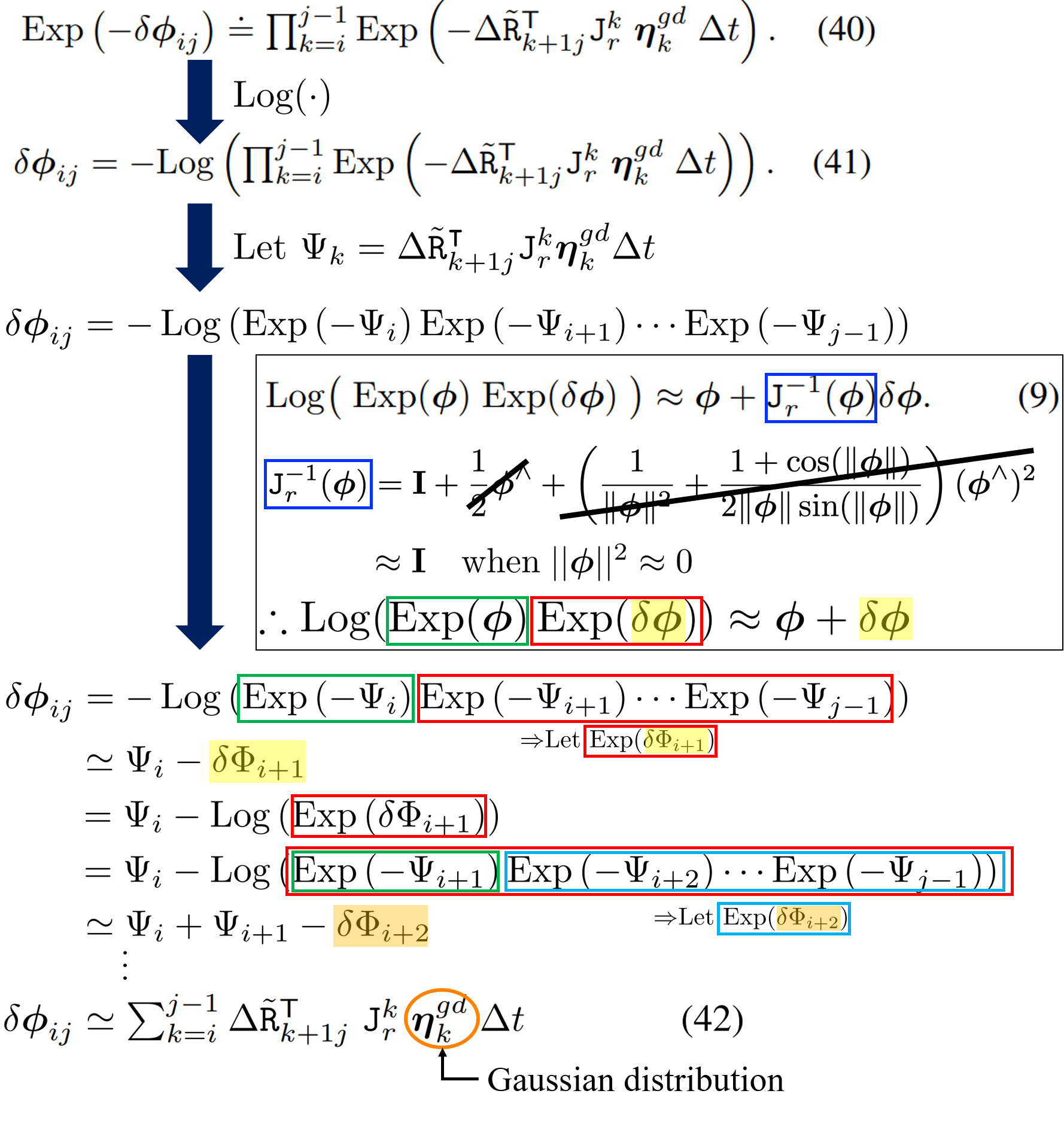
Gaussian의 합은 두 Guassian distribution이 independent and identically distributed (iid)하면 그 합 또한 Gaussian distribution을 따른다. 그런데 위의 IMU의 noise term인 \(\boldsymbol{\eta}^{gd}_k\)는 각 time step 별로 독립적이라고 가정할 수 있기 때문에 결론적으로 \(\delta \boldsymbol{\phi}_{ij}\)가 Gaussian distribution을 따른다는 것을 증명할 수 있다.

이를 통해 세 relative motion increments들은 아래처럼 모두 Gaussian 꼴을 따른다고 모델링이 가능하다:

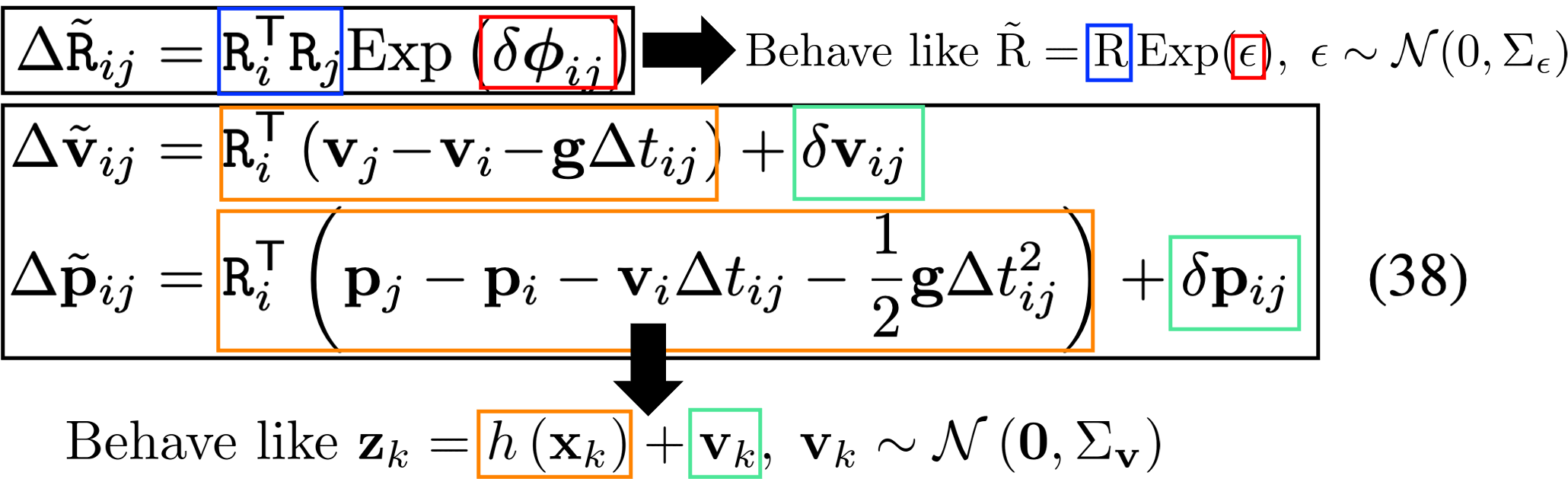
Uncertainty가 Gaussian distribution의 꼴이라는 말은 optimization의 결과가 Maximum a posteriori (MAP)의 최적값으로 estimate되는 것이 가능하다는 것을 뜻한다 (cf. Uncertainty가 gaussian의 꼴을 따르지 않으면 이는 그냥 non-linear optimization이라 부른다).

Bias Update

이렇게 relative motion increments term들을 이용해 factor graph 상에 constraint를 추가하는데, 이를 “IMU factor”라 부른다. IMU factor를 통해서 추가적으로 IMU의 keyframe 사이의 accelerator와 gyroscope의 biases 또한 parameter로 세팅하며 이를 optimization을 통해 update한다 (논문의 Section Ⅵ. E).

위의 수식 (48)은 factor graph 상에서 biases를 위한 residual term을 의미하는데, biases는 이전 time step의 biases과 그 크기가 비슷하다는 것을 기반으로 구성되어 있다. 이는 위에서 biases가 시간이 지남에 따라서 빠르게 변화하진 않는다는 가정에 합당한 term이라고 볼 수 있다.

결론

정리하자면 preintegration이라는 것은 “\(i\)번째 keyframe과 \(j\) keyframe 사이의 IMU data를 integration하여 세 relative motion increments와 biases term으로 구성된 하나의 factor를 생성하는 과정”이라고 요약할 수 있다. 여기까지 도달하는 데에 많은 수식 전개가 있었는데, 그렇다면 위의 수식들을 다 알아야 할까? 그렇지 않다. ㄴ 사실 Integration은 gtsam::PreintegratedImuMeasurements 클래스의 integrateMeasurement() 함수로 이미 구현이 되어 있어서 \(i\)와 \(j\) 사이의 IMU measurement를 위 함수에 입력으로 넣어주면 된다.

// imuIntegratorOpt_: `gtsam::PreintegratedImuMeasurements` class
imuIntegratorOpt_->integrateMeasurement(
    gtsam::Vector3(thisImu->linear_acceleration.x, thisImu->linear_acceleration.y, thisImu->linear_acceleration.z),
    gtsam::Vector3(thisImu->angular_velocity.x,    thisImu->angular_velocity.y,    thisImu->angular_velocity.z), dt);

그리고 relative motion increments에 대한 세 term과 biases term 또한 gtsam::ImuFactor라는 클래스에 preintegrated measurements를 대입해주면 알아서 계산하게 이미 잘 구현되어 있다. 아래는 LIO-SAM의 imuPreintegration.cpp 내부의 코드의 예제이다.

// graphFactors: `gtsam::NonlinearFactorGraph` class
const gtsam::PreintegratedImuMeasurements& preint_imu = dynamic_cast<const gtsam::PreintegratedImuMeasurements&>(*imuIntegratorOpt_);
gtsam::ImuFactor imu_factor(X(key - 1), V(key - 1), X(key), V(key), B(key - 1), preint_imu);
graphFactors.add(imu_factor);

따라서 implementation 관점에서 preintegration을 하기 위해 기억해야할 것을 정리하자면 아래와 같다.

주어져야 하는 것: LiDAR나 camera를 통해 추정한 \(i\) 번째 keyframe과 \(j\) 번째 keyframe의 pose. 이것들은 optimization을 할 때 prior factor로 사용됨.
계산해야 하는 것: \(i\)번째 keyframe과 \(j\)번째 keyframe 사이의 K개의 IMU data로부터 \(\Delta \tilde{\mathtt{R}}_{ij}\), \(\Delta \tilde{\mathbf{v}}_{ij}\), \(\Delta \tilde{\mathbf{p}}_{ij}\), \(\delta {\boldsymbol{\phi}}_{ij}\), \(\delta {\mathbf{v}_{ij}}\), \(\delta {\mathbf{p}}_{ij}\).
Optimization되는 것: IMU의 biases들과 prior factor들의 pose들

더 자세한 사항은 다음 글에서 코드를 line-by-line으로 살펴보며 설명한다.

IMU Preintegration Derivation 설명 시리즈입니다.