Introduction: XYZ? ZYX?
Rotation을 공부한 이라면 한번쯤 3D rotation이 XYZ, ZYX등 분해하고자하는 축의 순서에 따라 rotation의 표현 방식이 달라진다는 것을 알고 있을 것이다.
그런데 오늘 문득, 이 축의 순서가 변경되더라도 각도의 값이 동일하게 유지되는 건지(i.e., 즉 이 roll-pitch-yaw가 unique한 값으로 출력되는지) 궁금해졌다.
특히, 예전에 Eigen의 eularAngles 함수로 Eular angle을 구하게 되면 다소 부정확한 Euler angle을 구하게 되는 것을 경험했었다.
그래서 이 참에 Eigen, OpenCV, GTSAM에서 구해지는 각도를 비교해보고자 한다.
Experiments
그래서 아래와 같이 테스트를 해보았다:
#include <gtsam/geometry/Pose3.h>
#include <gtsam/geometry/Rot3.h>
#include <Eigen/Dense>
#include <opencv2/opencv.hpp>
#include <iostream>
void getRPYFromEigenMatrix3d(const Eigen::Matrix3d& mat, double& roll, double& pitch, double& yaw, const std::string order="zyx") {
if (order == "zyx") {
Eigen::Vector3d rpy = mat.eulerAngles(2, 1, 0);
yaw = rpy[0];
pitch = rpy[1];
roll = rpy[2];
} else if (order == "xyz") {
Eigen::Vector3d ypr = mat.eulerAngles(0, 1, 2);
roll = ypr[0];
yaw = ypr[2];
pitch = ypr[1];
}
}
void mat2rpy(const Eigen::Matrix3d& eigen_mat, double& roll, double& pitch, double& yaw) {
// Convert Eigen::Matrix3d to cv::Mat
cv::Mat cv_mat(3, 3, CV_64F);
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
cv_mat.at<double>(i, j) = eigen_mat(i, j);
}
}
// Use Rodrigues to convert rotation matrix to rotation vector
cv::Mat rot_vec;
cv::Rodrigues(cv_mat, rot_vec);
// Extract roll, pitch, yaw from rotation vector
roll = rot_vec.at<double>(0);
pitch = rot_vec.at<double>(1);
yaw = rot_vec.at<double>(2);
}
Eigen::Vector3d R2ypr(const Eigen::Matrix3d& R) {
Eigen::Vector3d n = R.col(0);
Eigen::Vector3d o = R.col(1);
Eigen::Vector3d a = R.col(2);
Eigen::Vector3d ypr(3);
double y = atan2(n(1), n(0));
double p = atan2(-n(2), n(0) * cos(y) + n(1) * sin(y));
double r = atan2(a(0) * sin(y) - a(1) * cos(y), -o(0) * sin(y) + o(1) * cos(y));
ypr(0) = y;
ypr(1) = p;
ypr(2) = r;
return ypr;
}
Eigen::Matrix3d generateRandomRotationMatrix() {
// Random number generator for rotation angle and axis
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<> dis(0.0, 1.0);
double x = dis(gen) * 2.0 - 1.0;
double y = dis(gen) * 2.0 - 1.0;
double z = dis(gen) * 2.0 - 1.0;
Eigen::Vector3d axis(x, y, z);
axis.normalize();
double angle = dis(gen) * 2.0 * M_PI;
Eigen::AngleAxisd angleAxis(angle, axis);
Eigen::Matrix3d rotationMatrix = angleAxis.toRotationMatrix();
return rotationMatrix;
}
int main() {
for (size_t i = 0; i < 10; ++i) {
Eigen::Matrix3d rotation = generateRandomRotationMatrix();
gtsam::Rot3 R = gtsam::Rot3(rotation);
double roll, pitch, yaw;
std::cout << "----------------------------------------" << std::endl;
getRPYFromEigenMatrix3d(rotation, roll, pitch, yaw);
std::cout << "[Eigen] Roll: " << roll << ", Pitch: " << pitch << ", Yaw: " << yaw << std::endl;
getRPYFromEigenMatrix3d(rotation, roll, pitch, yaw, "xyz");
std::cout << "[Eigen] Roll: " << roll << ", Pitch: " << pitch << ", Yaw: " << yaw << std::endl;
mat2rpy(rotation, roll, pitch, yaw);
std::cout << "[OpenCV] Roll: " << roll << ", Pitch: " << pitch << ", Yaw: " << yaw << std::endl;
auto vec = R.ypr();
std::cout << "[GTSAM] Roll: " << vec(2) << ", Pitch: " << vec(1) << ", Yaw: " << vec(0) << std::endl;
auto vec2 = R.rpy();
std::cout << "[GTSAM] Roll: " << vec2(0) << ", Pitch: " << vec2(1) << ", Yaw: " << vec2(2) << std::endl;
auto vec3 = R2ypr(rotation.matrix());
std::cout << "[Ours] Roll: " << vec3(2) << ", Pitch: " << vec3(1) << ", Yaw: " << vec3(0) << std::endl;
std::cout << "----------------------------------------" << std::endl;
}
return 0;
}
Results
아래와 같이 Eigen은 지멋대로(?) 나오고, OpenCV도 GTSAM과는 다른 값을 출력하는 것을 볼 수 있다.
----------------------------------------
[Eigen] Roll: 0.916619, Pitch: -1.11678, Yaw: 0.52429
[Eigen] Roll: 1.29984, Pitch: -0.0762302, Yaw: 1.18016
[OpenCV] Roll: 1.09269, Pitch: -0.813915, Yaw: 0.953083
[GTSAM] Roll: 0.916619, Pitch: -1.11678, Yaw: 0.52429
[GTSAM] Roll: 0.916619, Pitch: -1.11678, Yaw: 0.52429
[Ours] Roll: 0.916619, Pitch: -1.11678, Yaw: 0.52429
----------------------------------------
----------------------------------------
[Eigen] Roll: 0.676192, Pitch: 1.87551, Yaw: 2.25518
[Eigen] Roll: 1.33457, Pitch: 3.12706, Yaw: -1.76165
[OpenCV] Roll: -1.47043, Pitch: 1.22775, Yaw: 0.949887
[GTSAM] Roll: -2.4654, Pitch: 1.26608, Yaw: -0.886417
[GTSAM] Roll: -2.4654, Pitch: 1.26608, Yaw: -0.886417
[Ours] Roll: -2.4654, Pitch: 1.26608, Yaw: -0.886417
----------------------------------------
----------------------------------------
[Eigen] Roll: -0.165668, Pitch: 0.108446, Yaw: 0.13827
[Eigen] Roll: 2.96196, Pitch: 3.05849, Yaw: -2.98682
[OpenCV] Roll: -0.172739, Pitch: 0.0965931, Yaw: 0.146802
[GTSAM] Roll: -0.165668, Pitch: 0.108446, Yaw: 0.13827
[GTSAM] Roll: -0.165668, Pitch: 0.108446, Yaw: 0.13827
[Ours] Roll: -0.165668, Pitch: 0.108446, Yaw: 0.13827
----------------------------------------
----------------------------------------
[Eigen] Roll: -2.91913, Pitch: 2.46222, Yaw: 1.98467
[Eigen] Roll: 0.708182, Pitch: 0.0444666, Yaw: -1.25226
[OpenCV] Roll: 0.58398, Pitch: 0.478271, Yaw: -1.18085
[GTSAM] Roll: 0.222461, Pitch: 0.679375, Yaw: -1.15692
[GTSAM] Roll: 0.222461, Pitch: 0.679375, Yaw: -1.15692
[Ours] Roll: 0.222461, Pitch: 0.679375, Yaw: -1.15692
----------------------------------------
----------------------------------------
[Eigen] Roll: -2.95361, Pitch: -3.01765, Yaw: 3.05486
[Eigen] Roll: 0.17827, Pitch: -0.137615, Yaw: -0.0627147
[OpenCV] Roll: 0.182245, Pitch: -0.131632, Yaw: -0.0747167
[GTSAM] Roll: 0.187979, Pitch: -0.123945, Yaw: -0.0867317
[GTSAM] Roll: 0.187979, Pitch: -0.123945, Yaw: -0.0867317
[Ours] Roll: 0.187979, Pitch: -0.123945, Yaw: -0.0867317
----------------------------------------
----------------------------------------
[Eigen] Roll: -1.25587, Pitch: -0.340763, Yaw: 0.204595
[Eigen] Roll: 1.88125, Pitch: -2.84262, Yaw: 2.87885
[OpenCV] Roll: -1.20378, Pitch: -0.419062, Yaw: -0.0378063
[GTSAM] Roll: -1.25587, Pitch: -0.340763, Yaw: 0.204595
[GTSAM] Roll: -1.25587, Pitch: -0.340763, Yaw: 0.204595
[Ours] Roll: -1.25587, Pitch: -0.340763, Yaw: 0.204595
----------------------------------------
----------------------------------------
[Eigen] Roll: 1.44461, Pitch: 0.766666, Yaw: 0.424297
[Eigen] Roll: 1.46677, Pitch: 0.509763, Yaw: -0.719753
[OpenCV] Roll: 1.18871, Pitch: 0.887568, Yaw: -0.209468
[GTSAM] Roll: 1.44461, Pitch: 0.766666, Yaw: 0.424297
[GTSAM] Roll: 1.44461, Pitch: 0.766666, Yaw: 0.424297
[Ours] Roll: 1.44461, Pitch: 0.766666, Yaw: 0.424297
----------------------------------------
----------------------------------------
[Eigen] Roll: -3.13872, Pitch: 2.54813, Yaw: 0.65574
[Eigen] Roll: 0.387876, Pitch: -0.46117, Yaw: -2.39458
[OpenCV] Roll: 0.733224, Pitch: 0.245566, Yaw: -2.39459
[GTSAM] Roll: 0.00287387, Pitch: 0.59346, Yaw: -2.48585
[GTSAM] Roll: 0.00287387, Pitch: 0.59346, Yaw: -2.48585
[Ours] Roll: 0.00287387, Pitch: 0.59346, Yaw: -2.48585
----------------------------------------
----------------------------------------
[Eigen] Roll: 2.80058, Pitch: 2.94395, Yaw: 2.93077
[Eigen] Roll: 2.83916, Pitch: 2.88794, Yaw: 3.00377
[OpenCV] Roll: -0.317813, Pitch: 0.230687, Yaw: -0.174408
[GTSAM] Roll: -0.341014, Pitch: 0.197647, Yaw: -0.210819
[GTSAM] Roll: -0.341014, Pitch: 0.197647, Yaw: -0.210819
[Ours] Roll: -0.341014, Pitch: 0.197647, Yaw: -0.210819
----------------------------------------
----------------------------------------
[Eigen] Roll: -2.4009, Pitch: 1.22948, Yaw: 1.03062
[Eigen] Roll: 2.35147, Pitch: -1.21214, Yaw: -1.05822
[OpenCV] Roll: 2.39326, Pitch: 0.605415, Yaw: -1.91812
[GTSAM] Roll: -2.4009, Pitch: 1.22948, Yaw: 1.03062
[GTSAM] Roll: -2.4009, Pitch: 1.22948, Yaw: 1.03062
[Ours] Roll: -2.4009, Pitch: 1.22948, Yaw: 1.03062
----------------------------------------
분석 및 설명
1. Eigen 관련
Eigen의 EulerAngles.h는 아래와 같이 구현되어 있다 (여기 참조):
// This file is part of Eigen, a lightweight C++ template library
// for linear algebra.
//
// Copyright (C) 2008 Gael Guennebaud <gael.guennebaud@inria.fr>
//
// This Source Code Form is subject to the terms of the Mozilla
// Public License v. 2.0. If a copy of the MPL was not distributed
// with this file, You can obtain one at http://mozilla.org/MPL/2.0/.
#ifndef EIGEN_EULERANGLES_H
#define EIGEN_EULERANGLES_H
#include "./InternalHeaderCheck.h"
namespace Eigen {
template<typename Derived>
EIGEN_DEVICE_FUNC inline Matrix<typename MatrixBase<Derived>::Scalar,3,1>
MatrixBase<Derived>::eulerAngles(Index a0, Index a1, Index a2) const
{
EIGEN_USING_STD(atan2)
EIGEN_USING_STD(sin)
EIGEN_USING_STD(cos)
/* Implemented from Graphics Gems IV */
EIGEN_STATIC_ASSERT_MATRIX_SPECIFIC_SIZE(Derived,3,3)
Matrix<Scalar,3,1> res;
typedef Matrix<typename Derived::Scalar,2,1> Vector2;
const Index odd = ((a0+1)%3 == a1) ? 0 : 1;
const Index i = a0;
const Index j = (a0 + 1 + odd)%3;
const Index k = (a0 + 2 - odd)%3;
if (a0==a2)
{
res[0] = atan2(coeff(j,i), coeff(k,i));
if((odd && res[0]<Scalar(0)) || ((!odd) && res[0]>Scalar(0)))
{
if(res[0] > Scalar(0)) {
res[0] -= Scalar(EIGEN_PI);
}
else {
res[0] += Scalar(EIGEN_PI);
}
Scalar s2 = Vector2(coeff(j,i), coeff(k,i)).norm();
res[1] = -atan2(s2, coeff(i,i));
}
else
{
Scalar s2 = Vector2(coeff(j,i), coeff(k,i)).norm();
res[1] = atan2(s2, coeff(i,i));
}
// With a=(0,1,0), we have i=0; j=1; k=2, and after computing the first two angles,
// we can compute their respective rotation, and apply its inverse to M. Since the result must
// be a rotation around x, we have:
//
// c2 s1.s2 c1.s2 1 0 0
// 0 c1 -s1 * M = 0 c3 s3
// -s2 s1.c2 c1.c2 0 -s3 c3
//
// Thus: m11.c1 - m21.s1 = c3 & m12.c1 - m22.s1 = s3
Scalar s1 = sin(res[0]);
Scalar c1 = cos(res[0]);
res[2] = atan2(c1*coeff(j,k)-s1*coeff(k,k), c1*coeff(j,j) - s1 * coeff(k,j));
}
else
{
res[0] = atan2(coeff(j,k), coeff(k,k));
Scalar c2 = Vector2(coeff(i,i), coeff(i,j)).norm();
if((odd && res[0]<Scalar(0)) || ((!odd) && res[0]>Scalar(0))) {
if(res[0] > Scalar(0)) {
res[0] -= Scalar(EIGEN_PI);
}
else {
res[0] += Scalar(EIGEN_PI);
}
res[1] = atan2(-coeff(i,k), -c2);
}
else
res[1] = atan2(-coeff(i,k), c2);
Scalar s1 = sin(res[0]);
Scalar c1 = cos(res[0]);
res[2] = atan2(s1*coeff(k,i)-c1*coeff(j,i), c1*coeff(j,j) - s1 * coeff(k,j));
}
if (!odd)
res = -res;
return res;
}
} // end namespace Eigen
#endif // EIGEN_EULERANGLES_H
2. GTSAM 관련
GTSAM에서는 아래와 같이 RQ() 함수를 통해 roll, pitch, yaw를 구하는데,
// In https://github.com/borglab/gtsam/blob/164c35424b13057c10a261eb4c8b6343125dccc9/gtsam/geometry/Rot3.cpp
pair<Matrix3, Vector3> RQ(const Matrix3& A, OptionalJacobian<3, 9> H) {
// x is roll
const double x = -atan2(-A(2, 1), A(2, 2));
const auto Qx = Rot3::Rx(-x).matrix();
const Matrix3 B = A * Qx;
// y is pitch
const double y = -atan2(B(2, 0), B(2, 2));
const auto Qy = Rot3::Ry(-y).matrix();
const Matrix3 C = B * Qy;
// z is yaw
const double z = -atan2(-C(1, 0), C(1, 1));
const auto Qz = Rot3::Rz(-z).matrix();
const Matrix3 R = C * Qz;
...
xyz(), rpy(), ypr() 모두 위의 RQ 함수를 통해 구한 후, 그 순서만 바꿔서 출력해주기 때문에 무엇을 불러도 그 값이 동일하다.
Vector3 Rot3::ypr(OptionalJacobian<3, 3> H) const {
Vector3 q = xyz(H);
if (H) H->row(0).swap(H->row(2));
return Vector3(q(2),q(1),q(0));
}
3. Ours 관련
이 회전 decomposition은 Tait-Bryan angles의 ZYX 방식을 따른 것이다.
한 가지 신기한 점은,GTSAM 코드를 살펴보면 XYZ 순으로 계산했더라도 그 값이 R2ypr의 결과와 정확히 동일하다는 점이다.
즉, 단순히 decomposition의 순서에 따라 ZYX, XYZ로 불리는 것이 아니라 decomposition을 하는 기준 축을 어떻게 지정하느냐에 따라 그 결과가 ZYX인지 XYZ인지 결정되는 것 같다 (왜냐하면 XYZ 순으로 분해했는데소 ZYX 순서 decomposition과 각도 값이 동일하게 나왔기 때문):
수치 해석적 안정성
더욱 신기한 점은, Eigen의 eulerAngle로 구한 각도들이 수치적으로 불안정하다는 것이다.
// 입력값
R: [
0.682115, 0.531373, -0.502357;
-0.345114, 0.839599, 0.419488;
0.644683, -0.112768, 0.756087
]
----------------------------------------
// 분해된 각도들
[Eigen] Roll: 2.99354, Pitch: -2.44098, Yaw: 2.6732 // <- xyz
[Eigen] Roll: 2.63506, Pitch: -2.61527, Yaw: 2.47978 // <- zyx
[OpenCV] Roll: -0.303641, Pitch: -0.654363, Yaw: -0.500018
[GTSAM] Roll: -0.148056, Pitch: -0.700608, Yaw: -0.468394
[GTSAM] Roll: -0.148056, Pitch: -0.700608, Yaw: -0.468394 // <- zyx
[Ours] Roll: -0.148056, Pitch: -0.700608, Yaw: -0.468394 // <- zyx
위의 나온 출력값인 각도들을 활용해서 아래와 같이 online rotation convertor site에서 다시 입력값인 R을 역추적했을 때:
- Eigen with
XYZstyle
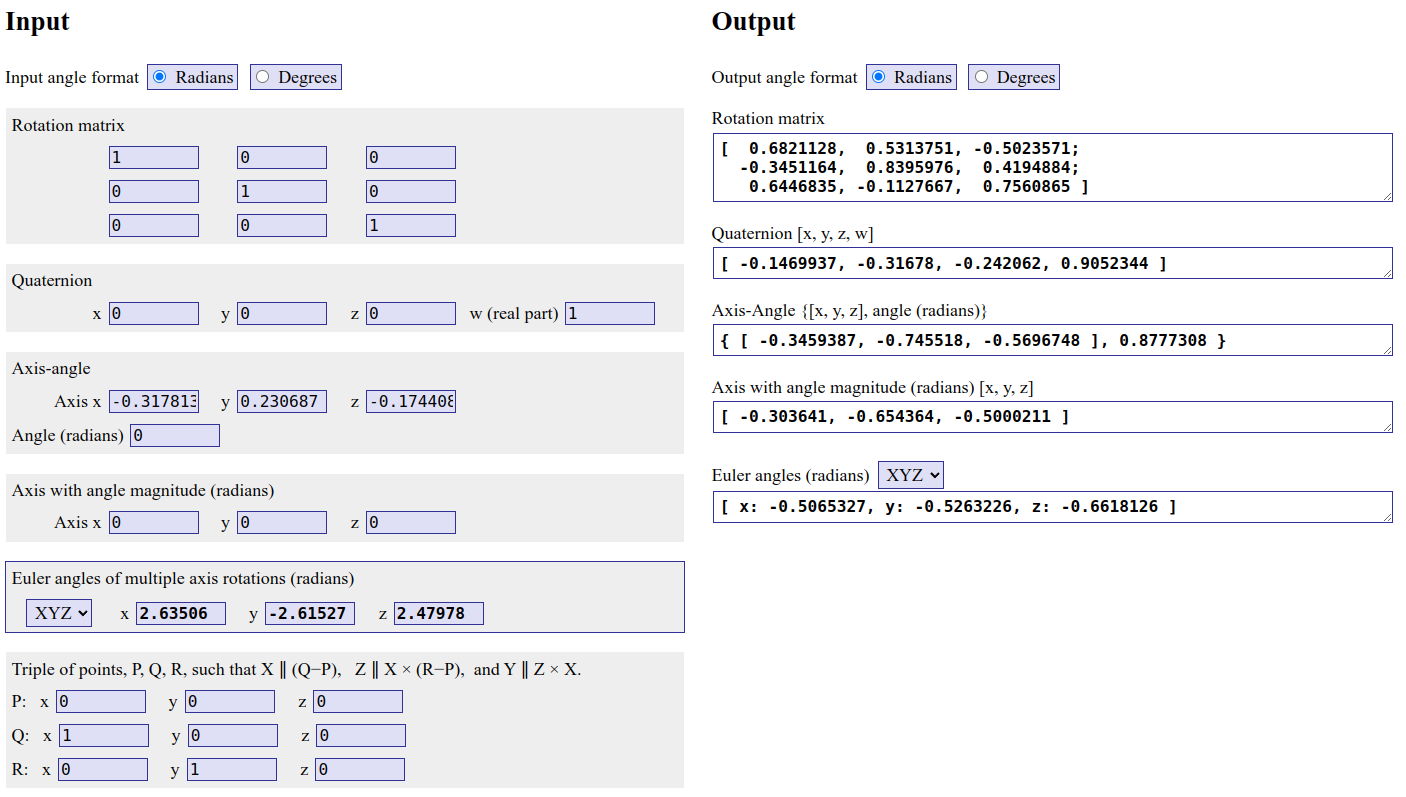
- Eigen with
ZYXstyle
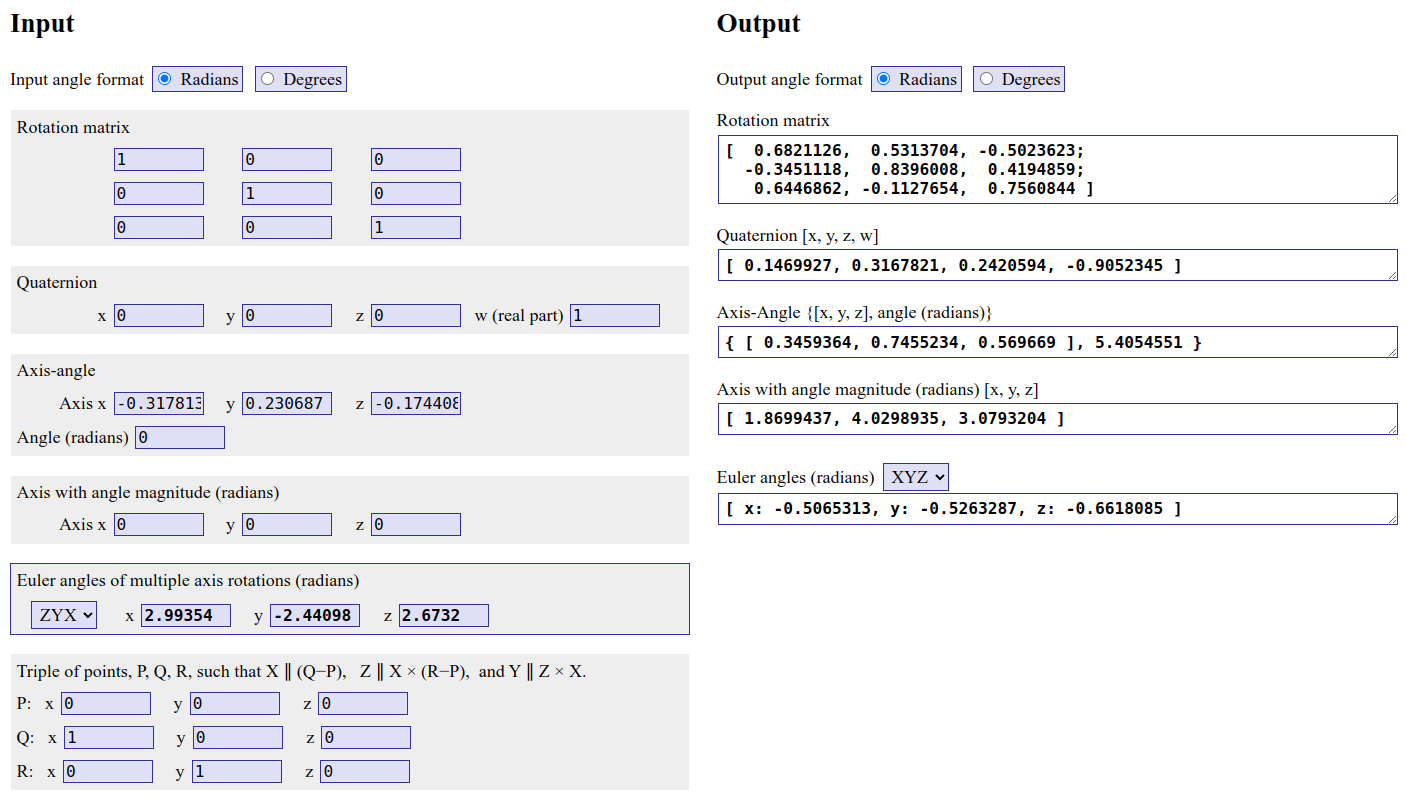
- From
R2yprfunction (which followsZYXformat)
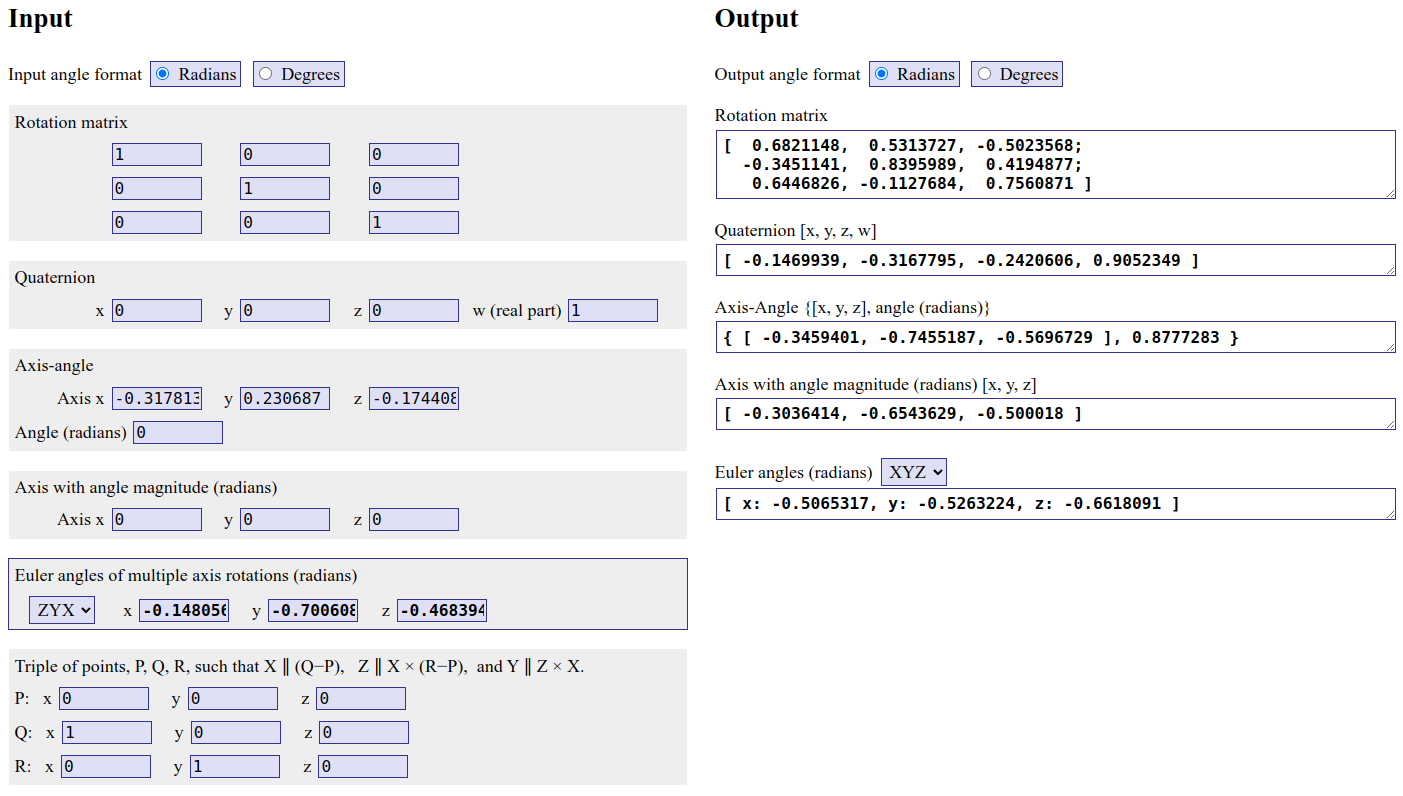
수치해석적 오차들이 굉장히 큰 것이 보이는가? 예로 들어, 0.682115가 되어야 하는 값이 Eigen으로 구한 각도를 썼을 때는 0.6821126이 나오는 반면, R2ypr를 통해 구한 각도에서 다시 rotation을 역생성하면 (1, 1)의 값이 0.6821148로 나오는 것을 볼 수 있다.
즉 0.0000025와 0.0000002로 거진 10배 큰 error가 나는 것을 볼 수 있다. 별거 아니라고 생각될 수 있다. 하지만 pose graph optimization 상에서 이 ypr와 rotation matrix의 변환을 적어도 각 state 별로 수 번에서 수 십번을 하게 될텐데, 그렇게 되면 이 에러가 필연적으로 쌓여서 포즈 에러가 누적될 수 있다.
결론
- Eigen의
eularAngle함수를 최대한 쓰지 말자. - ZYX, XYZ는 단순히 decompose하는 순서에 의거하기 보다는 분해하고자 하는 기준 축에 따라서 정의 되는 듯 하다 (GTSAM의 경우 X->Y->Z 순으로 각도를 decompose하더라도 ZYX 순서로 분해했을 때(i.e.,
R2ypr함수로 각을 얻었을 때)와 동일하게 결과가 나오기 때문)