GTSAM Tutorial 3. Skew Symmetric matrix 2차원에서 쉽게 이해하기

Introduction

나는 3차원에서의 설명을 하기 앞서 저차원에서 현상에 대한 이해를 설명하는 것을 선호하는 편인데, 오늘은 rotation의 skew symmetric matrix에 대해 쉽게 설명하고자 한다 (이전 글과 이어짐).

Derivative of Rotation Matrix

나와 유사한 교과 과정을 겪은 이라면 2차원의 rotation은 각도 \(\theta\)에 대한 표현식으로 나타낼 수 있고, 이는 코마신신코(요즘에는 고등학교 때 행렬 자체를 안 배운다고 하던데…)라는 것을 알고 있을 것이다:

\[\mathbf{R} = {R}(\theta) =\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\]

이를 손으로 직접 미분하면 아래와 같은 값을 구할 수 있다:

\[\frac{\partial R(\theta)}{\partial \theta}=\left[\begin{array}{cc} -\sin \theta & -\cos \theta \\ \cos \theta & -\sin \theta \end{array}\right]\]

그리고 이를 다시 rotation matrix \(R(\theta)\)로 표현하면 아래와 같이 표현할 수 있는데,

\[\frac{\partial R(\theta)}{\partial \theta}=R(\theta) \hat{\Omega}=\hat{\Omega}R(\theta) \; \; \text{where} \; \; \hat{\Omega}=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right] \; \; \; \; \text{(6)}\]

여기서 위의 \(\hat{\Omega}\)가 우리가 Lie algebra를 공부할 때 흔히 들었던 skew-symmetric matrix의 꼴을 띈다. 즉, 최종적으로 이전 글에서 수식 (5) \(\frac{\partial \mathbf{R}}{\partial \theta}\mathbf{x}\)의 \(\frac{\partial \mathbf{R}}{\partial \theta}\)에 수식 (6)을 대입해보면, \(\hat{\Omega}R(\theta)\mathbf{x}\)가 된다. 이는 \(\mathbf{x}\)를 \(R(\theta)\)로 회전시킨 후 skew-symmetric matrix를 곱한 것이 최종적으로 rotation matrix의 미분에 해당되는 값이라는 것을 알 수 있다.

Rotation에서 Skew-Symmetric Matrix 활용

즉, Skew-Symmetric Matrix는 rotation matrix의 변화량을 표현하는 데 있어 매우매우 중요한 수학적 tool이다. 만약 translation이었다면 우리는 변화량 \(\Delta\mathbf{t}\)가 단순히 덧셈을 통해(i.e., \(\mathbf{t} + \Delta \mathbf{t}\)) 값을 update할 수 있다는 것을 알고 있다. 그런데 회전의 경우에는 \(\mathbf{R}_1\mathbf{R}_2\)와 같이 곱하기로 값을 업데이트 하기 때문에, 원래라면 단순히 덧셈으로 증분을 표현할 수는 없을 것이다. 그렇다면 rotation의 증분은 어떻게 표현할 수 있을까?

어떤 미소 각 \(\delta_{\theta}\)에 대해 회전을 하는 rotation matrix는 다음과 같은데:

\[R(\delta_{\theta}) = \left[\begin{array}{cc} \cos \delta_{\theta} & -\sin \delta_{\theta} \\ \sin \delta_{\theta} & \cos \delta_{\theta} \end{array}\right]. \; \; \; \; \text{(7)}\]

수식 (7)에 쓰인 \(\delta_{\theta}\)는 굉장히 작은 각도 값이므로, \(\delta_{\theta} \simeq 0\)라고 가정할 수 있다(이를 small angle approximation이라 부름). 이를 통해 \(\cos \delta_{\theta} \simeq 1\), \(\sin \delta_{\theta} \simeq \delta_{\theta}\)로 근사가 가능하므로, (7)는 아래와 같이 간소화되어 표현이 가능하다:

\[R(\delta_{\theta}) \simeq \left[\begin{array}{cc} 1 & -\delta_{\theta} \\ \delta_{\theta} & 1 \end{array}\right] = \mathbf{I}_{2 \times 2} + \hat{\Omega}\delta_{\theta}.\; \; \; \; \text{(8)}\]

수식 (8)에 \(R(\theta)\)를 곱해 보자. 그러면 아래와 같은 수식이 전개된다:

\[R(\theta)R(\delta_{\theta}) \simeq R(\theta)(\mathbf{I}_{2 \times 2} + \hat{\Omega}\delta_{\theta}) = R(\theta) + \frac{\partial R(\theta)}{\partial \theta}\delta_{\theta}.\; \; \; \; \text{(9)}\]

아주 놀랍게도, 수식 (9)에서 볼 수 있듯이, 이 \(\hat{\Omega}\)를 활용하면, rotation의 변화량도 덧셈으로 표현을 하는게 가능해진다. 즉, 업데이트하고자 하는 각도의 양 \(\delta_{\theta}\)가 충분히 작다면, rotation의 상태 변화를 덧셈을 통해 표현이 가능해진다는 것을 확인할 수 있다. 그리고 이러한 특성은 뒤에 GTSAM에 쓰이는, H라 불리는, Jacobian의 수식 유도를 할 때 활발히 사용된다.

3차원에서 Skew-Symmetric Matrix 가볍게 접해보기

그리고 유도되는 과정을 쉽게 설명하기 위해 2차원에서만 설명을 진행하였는데, 3차원에서도 이는 똑같이 적용된다. 우리가 2차원의 회전의 미소 변화량을 \(\delta \theta\)로 편히 나타냈던 것 처럼, 3차원의 회전의 미소 변화량을 어떤 3D vector \(\boldsymbol{\omega} = (\omega_x, \omega_y, \omega_z)\)로 표현할 수 있다고 해보자. 그러면 3차원에서도 회전의 변화를 아래와 같이 표현할 수 있다:

\[\mathbf{R}R(\boldsymbol{\omega}) \simeq \mathbf{R}\left(\mathbf{I}_{3\times 3} + [\boldsymbol{\omega}]_\times\right),\; \; \; \; \text{(10)}\] \[[\boldsymbol{\omega}]_{\times} \triangleq\left[\begin{array}{ccc} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{array}\right].\]

그리고 이는 꼴이 수식 (9)와 정확히 일치한다. 수식 (10)이 복잡해보이는 이유는 아마 익숙치 않은 operator인 \([\cdot]_\times\) 때문일 것이다. 2차원에서는 회전축이 \(z\) 방향으로 고정되어 있었다보니 회전의 변화를 \(\hat{\Omega}\)와 단일 scalar 값의 곱으로 표현할 수 있었던 반면, 3차원에서는 임의의 방향에 대한 회전이 가능해지기 때문에 이를 표현하기 위해 위의 operator가 필요하다. 위의 \([\boldsymbol{\omega}]_\times\)를 풀어서 작성하면 아래와 같이 표현할 수 있는데:

\[[\boldsymbol{\omega}]_{\times} = \left[\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\omega_z + \left[\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{array}\right]\omega_y + \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right]\omega_x,\; \; \; \; \text{(11)}\]

3차원이어서 skew-symmetric matrix의 형태로 표현된 회전 축이 3개가 되었을 뿐, 원리 자체는 2차원에서의 미소 회전을 \(\hat{\Omega}\delta_{\theta} = \left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\delta_\theta\)로 표현할 때와 정확히 일치한다. 만약 \(\boldsymbol{\omega}\)에 \((0, 0, \delta_\theta)\)를 대입해보면 \([\boldsymbol{\omega}]_\times = \left[\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\delta_\theta\)로 표현해질 수 있게 되는데, 이는 2차원에서 \(\hat{\Omega}\delta_{\theta}\)의 꼴과 정확히 일치하는 것을 엿볼 수 있다.

따라서, 2차원이든 3차원이든 어떤 회전 \(\mathbf{R}\)의 증분을 해당 (i) rotation matrix \(\mathbf{R}\), (ii) skew-symmetric matrix 형태로 표현된 회전 축, 그리고 (iii) 회전량(i.e., scalar/vector의 형태)의 세 가지 항의 곱으로 나타낼 수 있다는 결론에 도달할 수 있다.

Skew-Symmetric Matrix의 물리적 의미

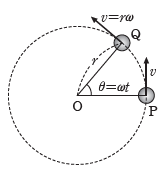
Circular Motion

(위의 그림은 여기에서 발췌)

그렇다면 이게 물리적으로 어떤 의미를 뜻할까? 이는 skew-symmetric matrix로 변형된 vector는 물리적으로 angular velocity를 의미하는데, 위의 그림의 검은 진한 화살표와 동일하다는 것을 알 수 있다. 즉, 회전에 접선 방향에 대한 움직임을 나타내는 것이라고 해석될 수 있다. 예로 들어서, rotation matrix로 회전된 값이 \((\frac{1}{2}, \frac{1}{2})\)라고 할 때, 여기에 \(\hat{\Omega}\)을 곱하게 되면 \((-\frac{1}{2}, \frac{1}{2})\) 값이 되는데, 이를 그려보면 정확히 원의 접선 vector와 일치하는 것을 볼 수 있다(대강 위의 그림의 \(\mathbf{Q}\) 의 화살표 방향 일치함).

3차원에서도 마찬가지로, 어떤 공간 상의 움직임에 접하는 평면 상의 vector를 뜻하게 된다. 사실 SLAM을 깊게 공부해보려 한 이라면 Lie group이니 Lie algebra이니 하는 말을 들어 보았을텐데, 이를 쉽게 해석해보자면 원래의 곱셈 연산을 통해 표현되는 어떤 값(group)을 덧셈/뺄셈을 통해 표현(algebra)할 수 있게 됨을 의미한다.

GTSAM Tutorial 시리즈입니다.