GTSAM Tutorial 10. numericalDerivative를 통한 Factor Debugging

Introduction

SLAM, 특히나 이런 optimization 관련 연구에서 가장 힘든 점이 무엇인지 아는가? 지금 내 graph에서 어디가 틀렸는지 알 턱이 없다는 것이다. 특히, factor 자체의 Jacobian을 잘 못 계산해줘서 optimization이 안되는 경우가 왕왕 생기기도 한다. 오늘은 내 factor가 제대로 동작하는지 디버깅하는 방법에 대해 알아보자.

How to Debug Your Factor Smartly?

GTSAM에서는 이를 위해 numericalDerivative라는 기능이 존재한다(필자도 이런 게 있는 줄 최근에 알았다. ‘Ceres Solver는 nemerical하게 알아서 Jacobian을 구해주는반면 GTSAM은 손수 계산해 줘야한다구욨!’이라고 외치고 다닌 멍청한 과거의 나…다시금 반성한다…).

아래는 내가 작성한 code snippet이다:

#include <gtsam/base/numericalDerivative.h>
#include <gtsam/geometry/Pose2.h>
#include <gtsam/inference/Symbol.h>
#include <gtsam/nonlinear/NonlinearFactor.h>
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
#include <gtsam/nonlinear/Values.h>
#include <gtsam/slam/BetweenFactor.h>

#include <Eigen/Dense>

using namespace gtsam;
using namespace std;

template <typename Factor, typename Error, typename V1, typename V2>
void evaluateFactor(const Factor& factor, const V1& v1, const V2& v2,
                    const Error& expected, double tol, double delta = 1.0e-5) {
  gtsam::Matrix H1_actual, H2_actual;
#if GTSAM_VERSION_MAJOR <= 4 && GTSAM_VERSION_MINOR < 3
  const auto actual = factor.evaluateError(v1, v2, H1_actual, H2_actual);
#else
  const auto actual = factor.evaluateError(v1, v2, &H1_actual, &H2_actual);
#endif

  const auto H1_expected = gtsam::numericalDerivative21<gtsam::Vector, V1, V2>(
      [&](const auto& v1, const auto& v2) {
        return factor.evaluateError(v1, v2);
      },
      v1, v2, delta);

  const auto H2_expected = gtsam::numericalDerivative22<gtsam::Vector, V1, V2>(
      [&](const auto& v1, const auto& v2) {
        return factor.evaluateError(v1, v2);
      },
      v1, v2, delta);

  std::cout << gtsam::assert_equal(Vector3(0.0, 0.0, 0.0), actual, tol)
            << std::endl;
  std::cout << gtsam::assert_equal(H1_expected, H1_actual, tol) << std::endl;
  std::cout << gtsam::assert_equal(H2_expected, H2_actual, tol) << std::endl;
}

int main() {
  // Define two Pose2 instances
  Pose2 pose1(1.0, 1.0, 0);
  Pose2 pose2(2.0, 3.0, M_PI / 4);

  Pose2 rel_pose = Pose2(1.0, 2.0, M_PI / 4);
  Vector3 error;
  error << 1.0, 2.0, M_PI / 4;

  static const gtsam::SharedNoiseModel& noise =
      gtsam::noiseModel::Isotropic::Variance(3, 1e-3);
  const auto factor = BetweenFactor<Pose2>(1, 2, pose1.between(pose2), noise);

  evaluateFactor(factor, pose1, pose2, error, 1.0e-5);
  return 0;
}

위와 같이 작성한 evaluateFactor라는 함수를 사용해서 현재 내가 짠 factor의 Jacobian이 수치적으로 맞는지 분석해주는 함수이다. 위의 gtsam::numericalDerivative21와 gtsam::numericalDerivative22에서 수치적으로 계산한 Jacobian인 H1_expected, H2_expected와 우리가 손으로 한땀한땀 작성한 H1_actual과 H2_actual이 동일한지 확인해볼 수 있다.

만약에 둘이 비교했을 때 같으면 gtsam::assert_equal이 1을 출력하고, 만약 값이 다르다면, 아마 아래와 같이

not equal:
예상 값과 실제 값
그리고 차이를 보여준 후
0

을 출력하고 마칠 것이다 (값 자체는 다른 factor를 구현할 때 촬영한 screenshot이고 노란색은 내가 임의로 추가해준 것이니, 값 자체들이 무슨 의미인지는 볼 필요 없다.):

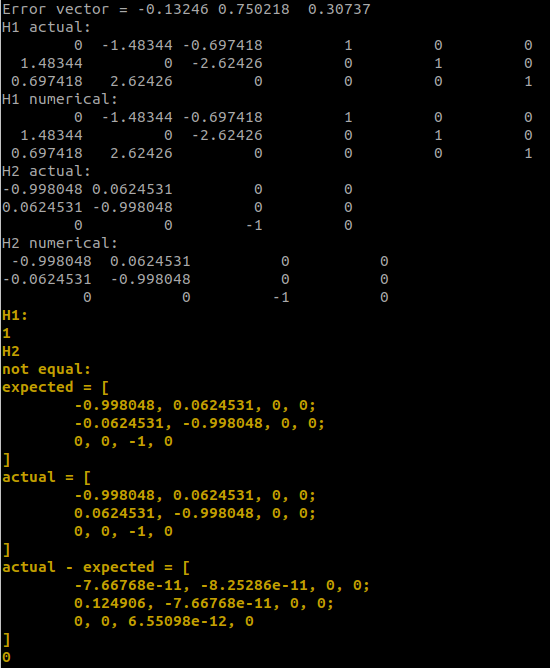
즉, 위의 예제 그림을 통해 현재 내가 actual Jacobian의 matrix의 (1, 0) 좌표 부분 해당하는 값에 minus 부호를 빠뜨린 실수를 발견할 수 있었다. 이처럼, 이 numericalDerivative를 쓰면 내가 계산한 Jacobian이 정확한 값인지 쉽게 확인할 수 있다! (GTSAM 짱짱!)

GTSAM Tutorial 시리즈입니다.