Generalized Iterative Closest Point (G-ICP)
최근에 measurements의 불확실성을 모델링해야할 일이 있어, Generalized Iterative Closest Point (G-ICP) 내부의 코드를 자세히 뜯어보게 되었다.
G-ICP는 대표적인 local registration 방법으로, 두 포인트 클라우드의 viewpoint가 충분히 가까이 있고 (약 2m 내외), 대부분의 영역이 충분히 overlap되어있는 경우에 사용한다.
코드레벨로 어떻게 사용하는지에 대해서는 여기에 잘 정리되어 있는데, 본 시리즈에서는 수식적인 레벨까지 이해하도록 분석을 한다.
글의 목표
PCL에서는
gicp.setInputSource(src);
gicp.setInputTarget(tgt);
gicp.align(*align);
를 통해 두 point cloud의 상대적 pose (x, y, z, roll, pitch, yaw)를 추정한다.
하지만 최근 Lie Algebra를 활용하여 SE(3) 상에서 relative pose를 추정하는 방법론들이 많이 제안이 되고 있다. Semantic ICP 논문에서는 G-ICP의 optimization을 위와 같이 (x, y, z, roll, pitch, yaw)에서 하는 게 아니라 special Euclidean group, i.e., SE(3),에서 cost를 direct하게 정의하는 것이 더 정확한 relative pose를 추정하는데 도움을 준다고 주장하고 있다.
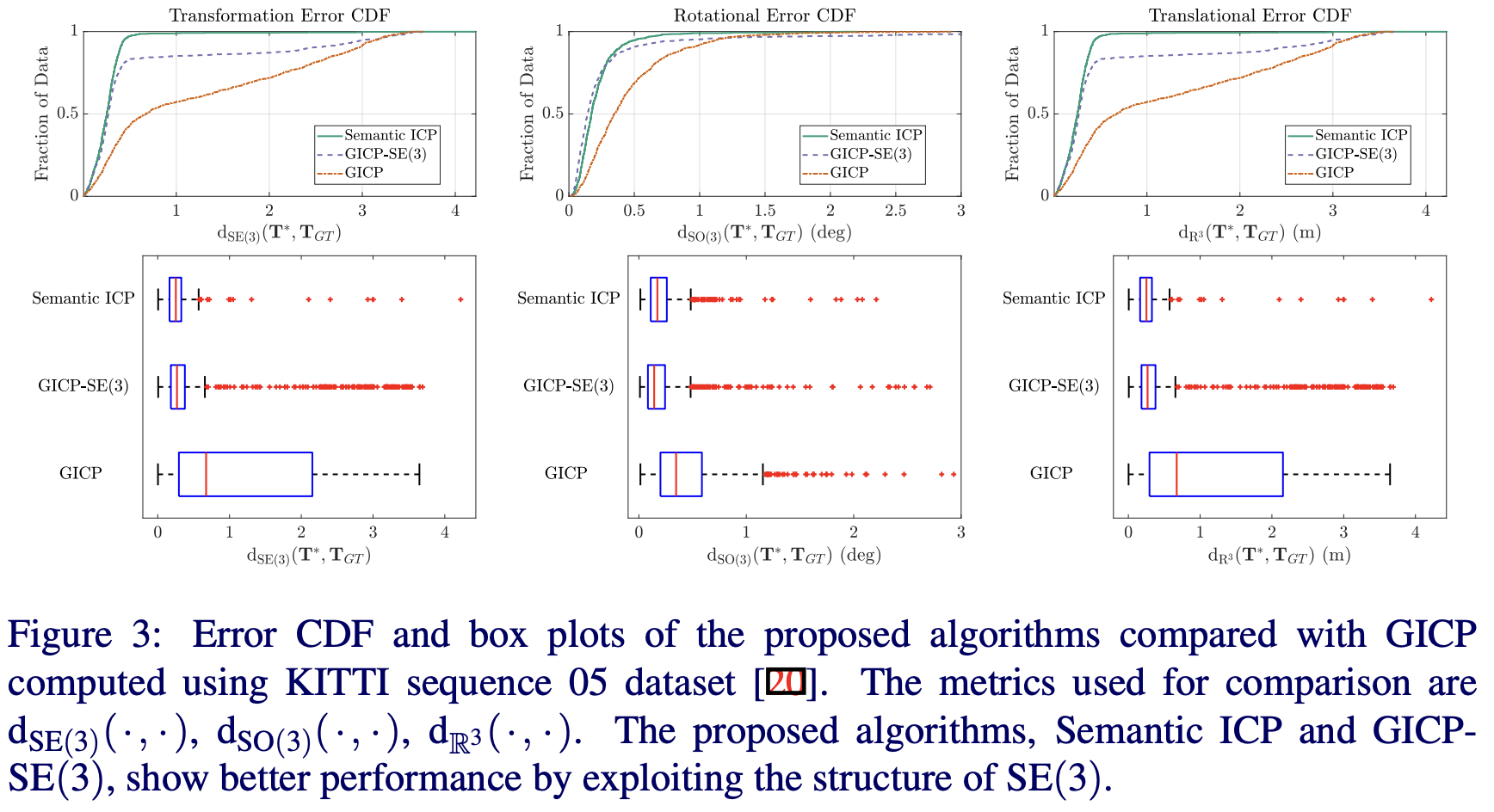
(원 논문에서 발췌. G-ICP < G-ICP SE(3) < Semantic ICP 순으로 더 우수한 성능을 보인다고 주장하고 있음. 젤 위의 row는 좌측상단에 가까울수록 더 좋고, 아래의 error bar plot은 error가 더 작을수록 더 좋음을 뜻함)
따라서 이 시리즈에서는
- i) PCL의 G-ICP에서 각 함수별로 내부적으로 어떤 일이 일어나고 있는지 line-by-line으로 살펴본다.
- ii) G-ICP SE(3)의 코드를 확인하여 special Euclidean group 상에서 어떻게 cost function을 정의하는 지 살펴본다.
를 목표로 한다.