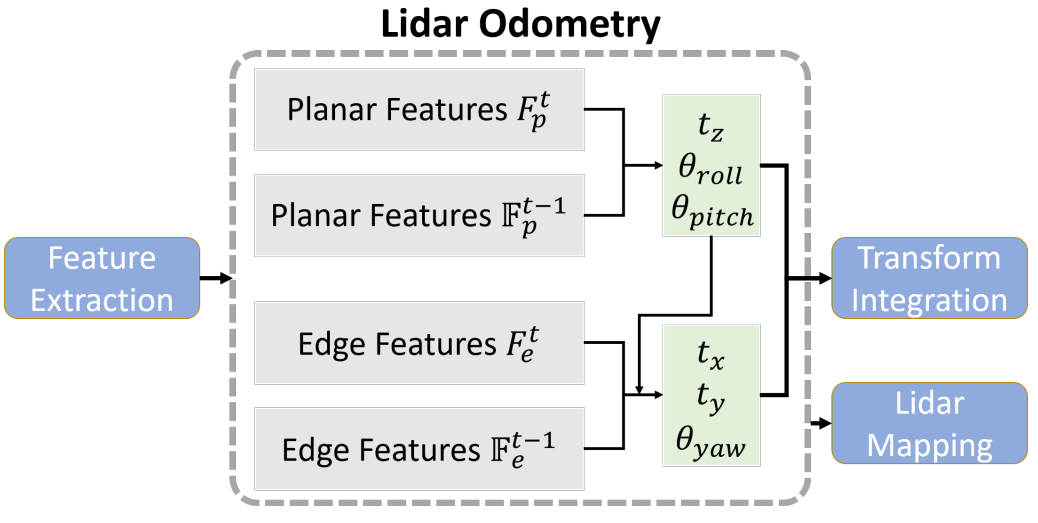
FeatureAssociation in LeGO-LOAM (3) Relative Pose Estimation via Two-stage Optimization

(cont’d)

Overview

최종적으로 t-1과 t의 feature를 구했으면, 주어진 feature들을 바탕으로 relative pose를 구한다. 흔히 알고 있듯이 planar feature를 통해 z, roll, pitch가 optimize하고 edge feature를 통해 x, y, yaw가 optimize하는, two-stage optimization 방식을 따른다.

다른 section과 다르게 이 부분에서는 Levenberg-Marquardt (LM) optimization을 하는 부분에 대한 코드 설명이 필요하다보니 좀 많이 수학수학해졌다 :(. 아래의 링크들이 도움이 되리라 생각된다.

updateInitialGuess()

updateInitialGuess() 함수에서는 IMU data가 들어오면 IMU data를 통해 구한 inital relative pose를 더해준다. 하지만 IMU를 쓰지 않으면 imuShiftFromStartX, imuShiftFromStartY, imuShiftFromStartZ, imuVeloFromStartX, imuVeloFromStartY, imuVeloFromStartZ 모두 다 계속 0이다. 즉, IMU 데이터가 들어오지 않으면 updateInitialGuess() 함수를 통해 transformCur가 업데이트되지는 않는다.

여기서 주의해야할 점은 초기 transformCur의 값은 t-2와 t-1 프레임 간의 pose로 할당되어 있다는 것이다. 다시 말해, 초기 값이 [0, 0, 0, 0, 0, 0]이 아니다! (물론 t=1과 t=2 사이의 pose를 추정하는 경우에는 [0, 0, 0, 0, 0, 0]으로 initialization되어 있음). 그 이유는 non-linear equation의 최적해를 구할 때는 iterative하게 optimization을 하는데, 이 때 주어진 초기값에 따라 성능이 많이 달라지게 된다. 이러한 문제를 해소하기 위해 좋은 initial 값을 지정해 주어야 한다.

따라서, 모바일 로봇의 경우 주로 앞-뒤로 움직이기 때문에 (어려운 말로는 non-holonomic motion을 주로 하기 때문에) 이전에 추정한 pose와 현재 추정해야할 pose의 경향성이 비슷하다는 전제하에 initial pose를 이전 time step에 추정한 pose를 할당해둔다.

void updateInitialGuess(){

    imuPitchLast = imuPitchCur;
    imuYawLast = imuYawCur;
    imuRollLast = imuRollCur;

    imuShiftFromStartX = imuShiftFromStartXCur;
    imuShiftFromStartY = imuShiftFromStartYCur;
    imuShiftFromStartZ = imuShiftFromStartZCur;

    imuVeloFromStartX = imuVeloFromStartXCur;
    imuVeloFromStartY = imuVeloFromStartYCur;
    imuVeloFromStartZ = imuVeloFromStartZCur;

    if (imuAngularFromStartX != 0 || imuAngularFromStartY != 0 || imuAngularFromStartZ != 0){
        transformCur[0] = - imuAngularFromStartY;
        transformCur[1] = - imuAngularFromStartZ;
        transformCur[2] = - imuAngularFromStartX;
    }

    if (imuVeloFromStartX != 0 || imuVeloFromStartY != 0 || imuVeloFromStartZ != 0){
        transformCur[3] -= imuVeloFromStartX * scanPeriod;
        transformCur[4] -= imuVeloFromStartY * scanPeriod;
        transformCur[5] -= imuVeloFromStartZ * scanPeriod;
    }
}

updateTransformation()

Pose estimation하는 부분은 자명하다. 크게 a) Correspondence 찾기와 b) Optimization을 통한 parameter update로 나눠지고, 이는 각각 planar feature과 edge feature에 대해 각각 행해진다.

void updateTransformation(){
    if (laserCloudCornerLastNum < 10 || laserCloudSurfLastNum < 100)
        return;
    // -------------------------------------------------------------------------
    // Optimization of t_z, roll, and pitch by using planar (surface) features 
    // -------------------------------------------------------------------------
    for (int iterCount1 = 0; iterCount1 < 25; iterCount1++) {
        laserCloudOri->clear();
        coeffSel->clear();

        findCorrespondingSurfFeatures(iterCount1);

        if (laserCloudOri->points.size() < 10)
            continue;
        if (calculateTransformationSurf(iterCount1) == false)
            break;
    }
    
    // ------------------------------------------------------------------
    // Optimization of t_x, t_y, and yaw by using corner (edge) features 
    // ------------------------------------------------------------------
    for (int iterCount2 = 0; iterCount2 < 25; iterCount2++) {

        laserCloudOri->clear();
        coeffSel->clear();

        findCorrespondingCornerFeatures(iterCount2);

        if (laserCloudOri->points.size() < 10)
            continue;
        if (calculateTransformationCorner(iterCount2) == false)
            break;
    }
}

순서는 surface features -> corner features 순으로 optimization을 진행하지만, 둘의 구조와 알고리즘 상의 방법론이 동일하기 때문에, 수식이 좀 더 쉬운 corner feature에 대해 먼저 설명한다.

a) Correspondence 찾기 findCorrespondingCornerFeatures(iterCount2)

void findCorrespondingCornerFeatures(int iterCount){

    int cornerPointsSharpNum = cornerPointsSharp->points.size();

    for (int i = 0; i < cornerPointsSharpNum; i++) {

        TransformToStart(&cornerPointsSharp->points[i], &pointSel);

        if (iterCount % 5 == 0) {

            kdtreeCornerLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis);
            int closestPointInd = -1, minPointInd2 = -1;

            if (pointSearchSqDis[0] < nearestFeatureSearchSqDist) {
                closestPointInd = pointSearchInd[0];
                int closestPointScan = int(laserCloudCornerLast->points[closestPointInd].intensity);

                float pointSqDis, minPointSqDis2 = nearestFeatureSearchSqDist;
                for (int j = closestPointInd + 1; j < cornerPointsSharpNum; j++) {
                    if (int(laserCloudCornerLast->points[j].intensity) > closestPointScan + 2.5) {
                        break;
                    }

                    pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) * 
                                 (laserCloudCornerLast->points[j].x - pointSel.x) + 
                                 (laserCloudCornerLast->points[j].y - pointSel.y) * 
                                 (laserCloudCornerLast->points[j].y - pointSel.y) + 
                                 (laserCloudCornerLast->points[j].z - pointSel.z) * 
                                 (laserCloudCornerLast->points[j].z - pointSel.z);

                    if (int(laserCloudCornerLast->points[j].intensity) > closestPointScan) {
                        if (pointSqDis < minPointSqDis2) {
                            minPointSqDis2 = pointSqDis;
                            minPointInd2 = j;
                        }
                    }
                }
                for (int j = closestPointInd - 1; j >= 0; j--) {
                    if (int(laserCloudCornerLast->points[j].intensity) < closestPointScan - 2.5) {
                        break;
                    }

                    pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) * 
                                 (laserCloudCornerLast->points[j].x - pointSel.x) + 
                                 (laserCloudCornerLast->points[j].y - pointSel.y) * 
                                 (laserCloudCornerLast->points[j].y - pointSel.y) + 
                                 (laserCloudCornerLast->points[j].z - pointSel.z) * 
                                 (laserCloudCornerLast->points[j].z - pointSel.z);

                    if (int(laserCloudCornerLast->points[j].intensity) < closestPointScan) {
                        if (pointSqDis < minPointSqDis2) {
                            minPointSqDis2 = pointSqDis;
                            minPointInd2 = j;
                        }
                    }
                }
            }

            pointSearchCornerInd1[i] = closestPointInd;
            pointSearchCornerInd2[i] = minPointInd2;
        }

        if (pointSearchCornerInd2[i] >= 0) {

            tripod1 = laserCloudCornerLast->points[pointSearchCornerInd1[i]];
            tripod2 = laserCloudCornerLast->points[pointSearchCornerInd2[i]];

            float x0 = pointSel.x;
            float y0 = pointSel.y;
            float z0 = pointSel.z;
            float x1 = tripod1.x;
            float y1 = tripod1.y;
            float z1 = tripod1.z;
            float x2 = tripod2.x;
            float y2 = tripod2.y;
            float z2 = tripod2.z;

            float m11 = ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1));
            float m22 = ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1));
            float m33 = ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1));

            float a012 = sqrt(m11 * m11  + m22 * m22 + m33 * m33);

            float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2));

            float la =  ((y1 - y2)*m11 + (z1 - z2)*m22) / a012 / l12;

            float lb = -((x1 - x2)*m11 - (z1 - z2)*m33) / a012 / l12;

            float lc = -((x1 - x2)*m22 + (y1 - y2)*m33) / a012 / l12;

            float ld2 = a012 / l12;

            float s = 1;
            if (iterCount >= 5) {
                s = 1 - 1.8 * fabs(ld2);
            }

            if (s > 0.1 && ld2 != 0) {
                coeff.x = s * la; 
                coeff.y = s * lb;
                coeff.z = s * lc;
                coeff.intensity = s * ld2;

                laserCloudOri->push_back(cornerPointsSharp->points[i]);
                coeffSel->push_back(coeff);
            }
        }
    }
}

위의 코드를 해석하자면 아래와 같이 크게 세 파트로 나뉘어진다.

i) TransformToStart(&cornerPointsSharp->points[i], &pointSel): 먼저 각 point는 initial pose를 활용하여 로봇의 motion으로 인한 error를 최소화한다. Point cloud 내의 한 point가 측정될 때에도 로봇은 계속 움직이기 때문에, 실제 측정된 원점이 제각각 달라질 수 있다. 따라서 이렇게 발생한 에러를 줄여주기 위해 아래와 같이 point를 transform하고, 이 행위를 deskewing이라고 부른다. 이를 위해 adjustDistortion()에서 미리 구해둔 scanPeriod * relTime를 활용하여 아래와 같이 각 point를 transform시킨다.

void TransformToStart(PointType const * const pi, PointType * const po)
{
    float s = 10 * (pi->intensity - int(pi->intensity));

    float rx = s * transformCur[0];
    float ry = s * transformCur[1];
    float rz = s * transformCur[2];
    float tx = s * transformCur[3];
    float ty = s * transformCur[4];
    float tz = s * transformCur[5];

    float x1 = cos(rz) * (pi->x - tx) + sin(rz) * (pi->y - ty);
    float y1 = -sin(rz) * (pi->x - tx) + cos(rz) * (pi->y - ty);
    float z1 = (pi->z - tz);

    float x2 = x1;
    float y2 = cos(rx) * y1 + sin(rx) * z1;
    float z2 = -sin(rx) * y1 + cos(rx) * z1;

    po->x = cos(ry) * x2 - sin(ry) * z2;
    po->y = y2;
    po->z = sin(ry) * x2 + cos(ry) * z2;
    po->intensity = pi->intensity;
}

위의 계산은 아래 수식과 동일하다 (변수 머리 위의 ~ 표시는 현재 deskwed되었음을 의미한다).

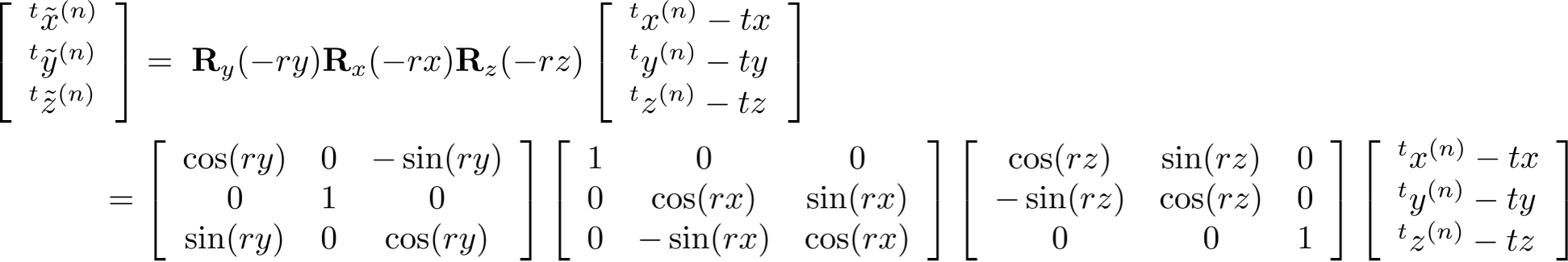(Q. 왜 음의 방향인가?: 실제로 t-1와 t를 푼 결과를 출력해보면 로봇이 앞쪽 방향으로 움직이고 있을 때 tz (ZXY좌표계에서 앞쪽 방향) 값이 음수로 도출된다. 즉 -1 * (음수)로 결론적으로는 양수값이 되어 상관 없긴 하다상관없으면 그냥 양수로 표현해주지ㅠㅜ.)

ii) Correspondence 찾기: 그 후, deskewing된 time t 상의 sharp한 corner feature와 가장 거리가 가까운, t-1 상의 두 corner feature를 찾는다. 여기서 kdtreeCornerLast의 입력 point cloud는 t-1의 cornerPointsLessSharp이다 (pose estimation이 완료되고 난 후 publishCloudsLast() 함수에서 세팅됨). 먼저 t-1에서 가장 가까운 점 1개를 찾은 후, 그 점을 기점으로 +-2.5 channel index 이내에 있는 corner feature를 그점으로 취급한다 (근데 코드 상에서 보면 +- check를 위->아래 순으로 체크하는 것 같다).

최종적으로는 가장 가까운 점과 그 다음 가까운 점이 아래와 같이 할당된다. 만약 두 점의 거리의 제곱이 주어진 파라미터 nearestFeatureSearchSqDist보다 크면 잘못된 pair라고 상정한다. 기본적으로 nearestFeatureSearchSqDist는 25m^2으로 설정되어 있다. 가장 가까운 포인트와 그 다음 가까운 포인트는 아래와 같이 index가 저장된다.

pointSearchCornerInd1[i] = closestPointInd;
pointSearchCornerInd2[i] = minPointInd2;

만약 할당이 제대로 되지 않았으면 -1이 세팅된다.

iii) Optimization에 필요한 values 세팅: 성공적으로 correspondence를 찾았으면 이제 향후 optimization에 필요한 값들을 세팅한다. 크게 아래의 세가지를 설정한다 (※수학주의).

1) Point-to-line distance

먼저 point-to-line distacne (아래의 ld2)가 계산된다. 엄밀히 말하자면, 외적(cross product)를 통해 두 line이 일치하는 정도를 측정한다. 외적을 하게 되면 크기x크기xsin(사잇각)이 되는데, 따라서 time t 상의 타겟 포인트와 t-1 상에서 타겟 포인트와 가장 가까운점과 그 다음 가까운 점을 각각 이은 두 선이 일치하는 쪽으로 향후에 optimize되는 것이다. 즉, 한 세 점이 한 직선 위에 놓여졌을 때 distance가 0이 된다. 수식을 전개하기 위해 아래 그림으로 대체한다.

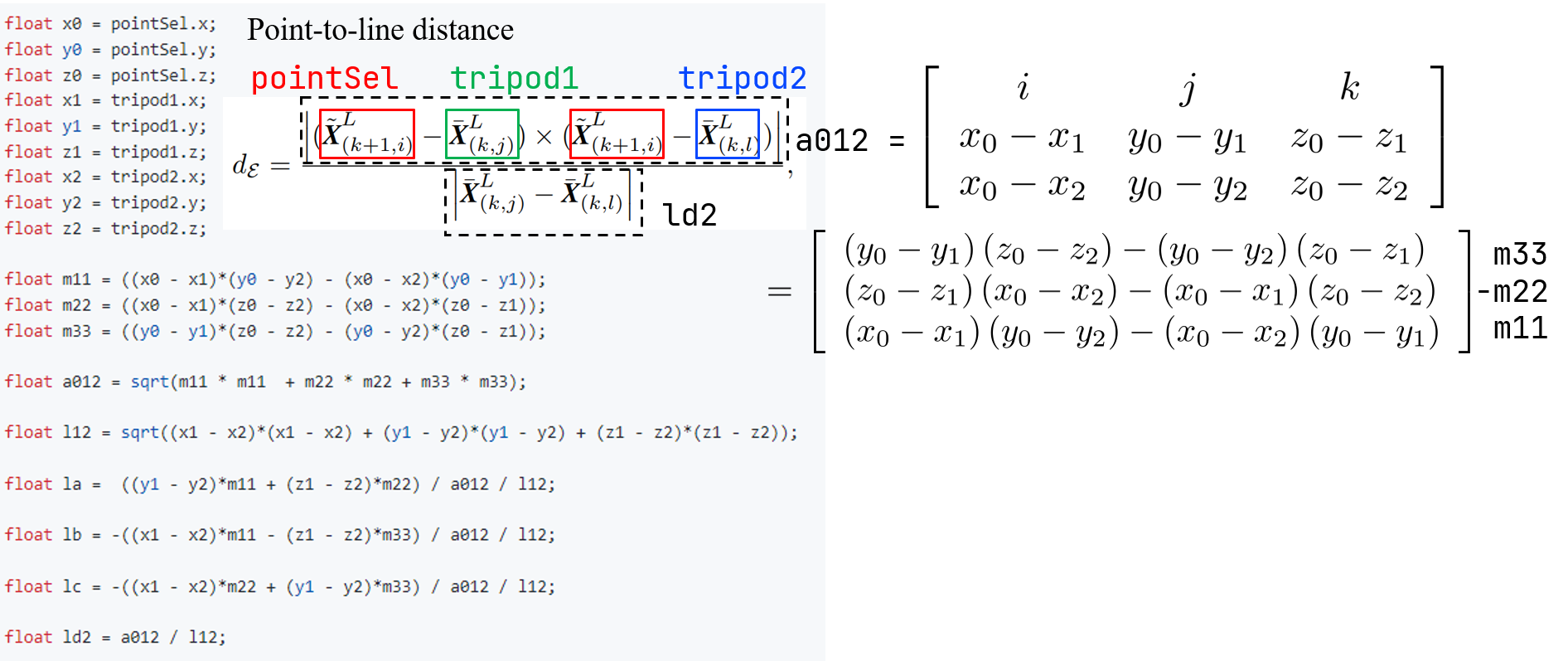(위의 수식에서 k+1이 본 글의 t와 대응되고, L은 LiDAR sensor frame임을 나타낸다.)

2) Jacobian term

그 후, optimization에 필요한 jacobian term을 미리 구해둔다. 위 코드 상에 la, lb, lc를 갑자기 계산하는 것이 무엇인지 명확히 나타나 있지 않고 설명해주는 글이 거의 없는데, 저 term은 향후에 optimization을 할 때 chain rule을 통해 jacobian term을 표현할 때 필요한 term들이다. 이를 이해하려면 먼저 non-linear equation을 iterative estimation method 기반으로 optimization하는 과정에 대해 이해해야 한다.

정리하자면 아래와 같고, 한 줄 요약하자면 optimization을 하려면 jacobian matrix J가 필요하다는 것을 알 수 있다.

Corner feature 같은 경우에는 아래와 같이 yaw, x, y (하지만 좌표축이 ZXY로 변했음을 기억하자. 따라서 ry (yaw 회전), tx (왼쪽), tz (앞쪽)으로 표현되고, 이 변수들의 미소 변화량을 구하는 것이 매 iterative estimation의 목표이다)의 변화량이 우리가 구하고자 하는 파라미터, i.e. △,가 된다. 하지만 현재 우리가 계산한 point-to-line distance는 deskewed point에 대한 함수로 표현될 뿐 ry, tx, tz로 직접적으로 표현되지 않는다. 따라서 point-to-line distance를 구하는 수식을 f라 표현했을 때, jacobian matrix의 각 term을 chain rule을 통해 아래와 같이 표현해주어야 한다 (아래의 1, 2, and 3).

정리하자면, ry, tx, tz에 대한 f의 partial derivative를 직접적으로 구할 수 없기 때문에 deskwed point의 x, y, z를 매개변수 삼아 상관관계를 표현하는 것이 가능해진다.

3) Alternative weighting

또한 각 distance에 대한 weight가 아래와 같이 매겨진다.

float s = 1;
if (iterCount >= 5) {
    s = 1 - 1.8 * fabs(ld2);
}

if (s > 0.1 && ld2 != 0) {
    coeff.x = s * la; 
    coeff.y = s * lb;
    coeff.z = s * lc;
    coeff.intensity = s * ld2;

    laserCloudOri->push_back(cornerPointsSharp->points[i]);
    coeffSel->push_back(coeff);
}

해석하자면,

  • 초기 5번 iteration 동안은 모든 distance들에 대해 s=1로 세팅하여 모든 measurements의 중요한 정도 (weight)를 균등하게 둔다.
  • 5번 이후에는 ld2의 크기에 따라 weight를 달리하는데, 특히 0.1이하의 경우에는 향후 optimization에 사용하지 않는다. s에 0.1을 대입하고 전개하면 저 조건문은 ld2가 0.5m 이하인 점들만 유효한 measurements로 여긴다고 해석할 수 있다. 이는 아주 reasonable한데, 왜냐하면 주로 모바일 로봇들이 1~3m/s로 움직이니, 0.1초 당 최대 0.3m 정도가 이동 가능하다고 가정할 수 있기 때문이다. 따라서 적어도 point-to-line distance가 0.5m 이내의 점들이 유효한 pair이고 그 이외의 점들은 extreme outliers일 가능성이 크기 때문에 위와 같은 weight를 세팅한다 (참고: 이렇게 매 iteration마다 weight를 다르게 주며 optimization하는 행위를 iteratively reweighted least squares라고도 부른다).

b) Optimization을 통한 parameter update calculateTransformationCorner(iterCount2)

Correspondences를 추정한 후, time t에서의 cornerPointsSharp에서 유효하다고 판단되어 선별된 laserCloudOri을 입력으로 하여 optimization을 진행한다. 전체 코드는 아래와 같고, transformation matrix를 구하는 과정은 다시 네 파트로 쪼개지는데, i) jacobian matrix 계산, ii) Ax=b 꼴 least square로 풀기, iii) degeneracy check, iv) 수렴했는지 판단으로 구성되어 있다.

bool calculateTransformationCorner(int iterCount){

    int pointSelNum = laserCloudOri->points.size();

    cv::Mat matA(pointSelNum, 3, CV_32F, cv::Scalar::all(0));
    cv::Mat matAt(3, pointSelNum, CV_32F, cv::Scalar::all(0));
    cv::Mat matAtA(3, 3, CV_32F, cv::Scalar::all(0));
    cv::Mat matB(pointSelNum, 1, CV_32F, cv::Scalar::all(0));
    cv::Mat matAtB(3, 1, CV_32F, cv::Scalar::all(0));
    cv::Mat matX(3, 1, CV_32F, cv::Scalar::all(0));

    float srx = sin(transformCur[0]);
    float crx = cos(transformCur[0]);
    float sry = sin(transformCur[1]);
    float cry = cos(transformCur[1]);
    float srz = sin(transformCur[2]);
    float crz = cos(transformCur[2]);
    float tx = transformCur[3];
    float ty = transformCur[4];
    float tz = transformCur[5];

    float b1 = -crz*sry - cry*srx*srz; float b2 = cry*crz*srx - sry*srz; float b3 = crx*cry; float b4 = tx*-b1 + ty*-b2 + tz*b3;
    float b5 = cry*crz - srx*sry*srz; float b6 = cry*srz + crz*srx*sry; float b7 = crx*sry; float b8 = tz*b7 - ty*b6 - tx*b5;

    float c5 = crx*srz;

    for (int i = 0; i < pointSelNum; i++) {

        pointOri = laserCloudOri->points[i];
        coeff = coeffSel->points[i];

        float ary = (b1*pointOri.x + b2*pointOri.y - b3*pointOri.z + b4) * coeff.x
                  + (b5*pointOri.x + b6*pointOri.y - b7*pointOri.z + b8) * coeff.z;

        float atx = -b5 * coeff.x + c5 * coeff.y + b1 * coeff.z;

        float atz = b7 * coeff.x - srx * coeff.y - b3 * coeff.z;

        float d2 = coeff.intensity;

        matA.at<float>(i, 0) = ary;
        matA.at<float>(i, 1) = atx;
        matA.at<float>(i, 2) = atz;
        matB.at<float>(i, 0) = -0.05 * d2;
    }

    cv::transpose(matA, matAt);
    matAtA = matAt * matA;
    matAtB = matAt * matB;
    cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);

    if (iterCount == 0) {
        cv::Mat matE(1, 3, CV_32F, cv::Scalar::all(0));
        cv::Mat matV(3, 3, CV_32F, cv::Scalar::all(0));
        cv::Mat matV2(3, 3, CV_32F, cv::Scalar::all(0));

        cv::eigen(matAtA, matE, matV);
        matV.copyTo(matV2);

        isDegenerate = false;
        float eignThre[3] = {10, 10, 10};
        for (int i = 2; i >= 0; i--) {
            if (matE.at<float>(0, i) < eignThre[i]) {
                for (int j = 0; j < 3; j++) {
                    matV2.at<float>(i, j) = 0;
                }
                isDegenerate = true;
            } else {
                break;
            }
        }
        matP = matV.inv() * matV2;
    }

    if (isDegenerate) {
        cv::Mat matX2(3, 1, CV_32F, cv::Scalar::all(0));
        matX.copyTo(matX2);
        matX = matP * matX2;
    }

    transformCur[1] += matX.at<float>(0, 0);
    transformCur[3] += matX.at<float>(1, 0);
    transformCur[5] += matX.at<float>(2, 0);

    for(int i=0; i<6; i++){
        if(isnan(transformCur[i]))
            transformCur[i]=0;
    }

    float deltaR = sqrt(
                        pow(rad2deg(matX.at<float>(0, 0)), 2));
    float deltaT = sqrt(
                        pow(matX.at<float>(1, 0) * 100, 2) +
                        pow(matX.at<float>(2, 0) * 100, 2));

    if (deltaR < 0.1 && deltaT < 0.1) {
        return false;
    }
    return true;
}

i) jacobian matrix 계산: 이전에 구해둔 la, lb, lc와 현재 n번째 point에 대한 partial derivative를 활용해서 jacobian matrix의 각 요소에 대해서 계산한다. 증명은 아래와 같고, 수식과 대응되는 부분은 사각형으로 표시해두었다.

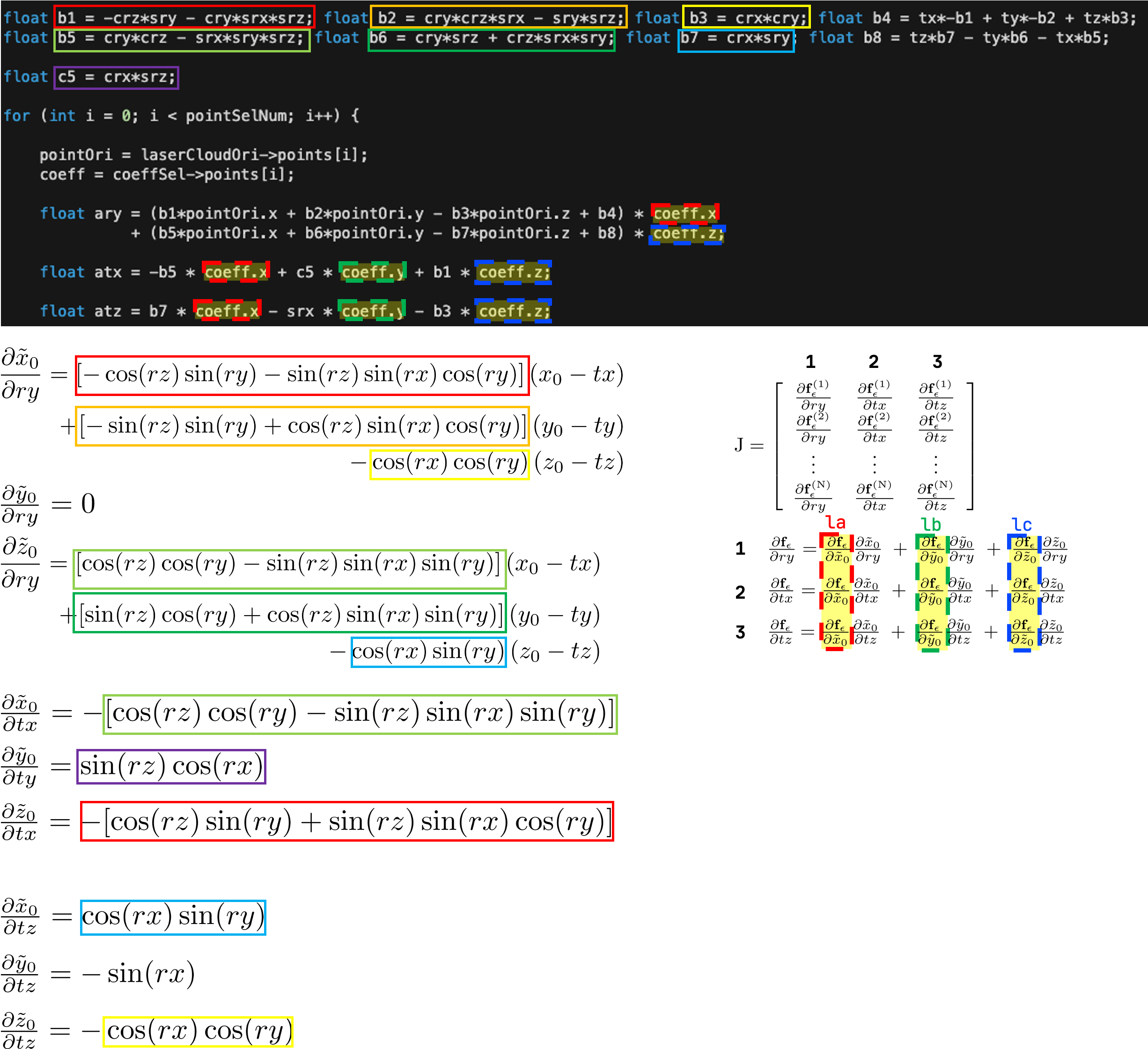
ii) Ax=b 꼴 matrix least square로 풀기: 그 후, 위에서 말했던 Ax=b 꼴의 J△=-b를 풀면 최적의 미소 변화량에 대해 구할 수 있다. 위의 코드에서 -b에 0.05가 곱해져 있는 것은 J△=-b을 통해 optimization할 때 그 변화의 폭이 너무 크지 않게 하기 위함이다. Iterative method는 현재 변수에 대해서 locally linear하다는 가정 하에 진행되는데, 변화량이 너무 크게 되면 가정과 맞지 않게 되기 때문에 이를 방지해주어야 한다.

iii) degeneracy check: 하지만 위에 같이 A가 정방 행렬이 아닌 경우에는 Ax=b 꼴의 수식을 풀 때는 양 변에 A^T를 곱해준 후, A^T*A를 정방 행렬으로 만든 후, pseudo-inverse를 통해 해를 푼다. 그런데, 가끔 A^T*A의 역행렬이 존재하지 않는 경우가 있는데, 이 isDegenerate는 이를 체크하기 위함이다. 실제로 코드를 돌려보면 좋은 환경에서는 이러한 degeneracy가 잘 일어나지 않는다.

iv) 수렴했는지 판단: 최종적으로 deltaR와 deltaT가 너무 작은 경우에는 수렴했다고 판단한다. 현재 코드 상에는 변화량의 각도가 0.1도 이내이거나 translation이 0.001m인 경우에 optimization을 중단하게 되어 있다.

Plane feature도 위와 똑같은 process로 똑같고, 다른 점은 point-to-plane distance를 구한다는 점이다. 연습문제로 삼아서 스스로 전개해보길 추천한다.

그 후…

그 후 구한 t-1과 t간의 relative pose를 integrateTransformation() 함수에서 축적하여 (0, 0, 0)으로부터 t까지의 relative pose를 transformSum에 저장하고, publishOdometry에서 ZXY 좌표계에서 다시 XYZ 좌표계로 변환 후 pose를 publish해준다. 자명하므로 생략.

마치며

지금까지 LeGO-LOAM의 핵심적인 부분에 대해서 line-by-line으로 살펴보았다. 개인적인 의견으로는 LeGO-LOAM의 꽃은 바닥으로부터 planar feature를 뽑고, non-ground로부터 corner feauture를 각각 뽑은 후 two-stage optimization을 통해 pose를 구하는 부분이라고 생각한다. 하지만 이렇게 decoupling하는 것은 trade-off가 있다. 먼저, a) 연산량을 줄여주고 b) oulier의 예기치 못한 error를 projection하여 outlier를 suppresion해주는 장점이 있다. 단점이라하면, (x, y, z, roll, pitch, yaw)은 실상 서로 독립적이지 않기 때문에 이렇게 two-stage로 따로따로 optimization을 하면 optimization이 종료되었더라도 미세하게 pose가 완전히 optimization해지지 못할 우려가 있다는 점이다. 그렇기에 논문에 보면 속도적인 측면에서 개선이 많이 되었음을 강조함으로써 (i7과 small form factor pc 둘다 실험을 하는 등) contribution을 가져간 것이 눈에 띈다.

MapOptimization 같은 경우에는 뽑은 feature들을 활용하여 어떻게 submap을 관리할지에 대한 테크니컬한 부분이 많아 생략한다 (time t와 t-1~t-T 간의 상관관계를 추정함). 무엇보다도 LIO-SAM에서 코드가 좀 더 정돈되었기 때문에, LeGO-LOAM의 MapOptimization을 보고 공부하기 보다는 LIO-SAM의 뒷부분이 어떻게 되어있는 지 살펴보는 것을 추천한다.

LeGO-LOAM의 line-by-line 설명 시리즈입니다.

  1. LeGO-LOAM-Line-by-Line-1.-Introduction: Preview and Preliminaries
  2. LeGO-LOAM-Line-by-Line-2.-ImageProjection-(1): Range Image Projection & Ground Removal
  3. LeGO-LOAM-Line-by-Line-2.-ImageProjection-(2): Cloud Segmentation using Clustering
  4. LeGO-LOAM-Line-by-Line-3.-FeatureAssociation-(1): Ready for Feature Extraction
  5. LeGO-LOAM-Line-by-Line-3.-FeatureAssociation-(2): Corner and Planar Feature Extraction
  6. LeGO-LOAM-Line-by-Line-3.-FeatureAssociation-(3): Relative Pose Estimation via Two-stage Optimization